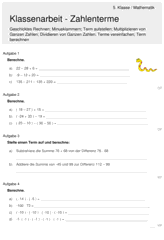
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 1
Schriftliche Rechnungen bitte auf einem Extrablatt!
1. Berechne folgenden Term!
[(-8) • (-9) + (-54) : 9] • 10 – 2 • 112 = __________________
2. Berechne!
a. 10 + ( 51 - 3 · 5 ) : 4 = ___ b. 50 - 5 · 7 = ___
c. 100 - ( 16 + 3 · 8 ) + 4 · 12 = ___ d. [ 18 + ( 3 · 12 - 6 · 5 ) ] · 8 = ___
3. Setze in den Gleichungen die Klammern, so dass die angegebenen
Ereignisse richtig sind!
a. 16 + 14 · 2 = 60 b. 10 · 7 - 2 + 3 = 53
4. Eine Klasse mit 27 Schülerinnen und Schülern fährt zur Eisenbahn.
Die Lehrerin sammelt von jedem 12 € ein. Sie bezahlt für die Schülergruppe
insgesamt 287,55 €.
Wie viel Geld bekommt jedes Kind zurück? Schreibe einen Term oder
rechne in einzelnen Schritten!
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
5. Schreibe als Term und berechne dann!
a) Multipliziere die Summe aus 12 und 19 mit der Differenz der Zahlen 444
und 435.
b) Dividiere das Produkt der Zahlen 4 und 14 durch die Differenz der Zahlen
166 und 159.
6. Schreibe zuerst die Aufgabe ins Heft und berechne dann
a) Der Minuend ist 156, der Subtrahend 92. Wie heißt das
Ergebnis?
b) Berechne den Quotienten von 192 und 17.
c) Berechne das Produkt von 36 und 3.
d) Durch welche Zahl muss man 180 dividieren, um 36 zu
erhalten?
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 2
1. Stelle den zugehörigen Rechenterm auf und berechne:
a) Addiere zur Summe der Zahlen 150 und 75 deren Differenz!
___________________________________________________________________________
___________________________________________________________________________
b) Subtrahiere von der Differenz der Zahlen 283 und 156 die Summe
der Zahlen 37 und 78
___________________________________________________________________________
___________________________________________________________________________
c) Subtrahiere die Differenz von178 und 94 von der Summe aus 248 und 132
___________________________________________________________________________
___________________________________________________________________________
d) Subtrahiere die Differenz der Zahlen 37 und 28 von deren Summe
___________________________________________________________________________
___________________________________________________________________________
2. Berechne und gib die Aufgabe in Wortform an!
a) (99 + 15) - (33 - 19) =
___________________________________________________________________________
___________________________________________________________________________
b) (82 - 19) - 18 =
___________________________________________________________________________
___________________________________________________________________________
c) 100 - (82 - 19 ) =
___________________________________________________________________________
___________________________________________________________________________
d) (12 + 18) - (28 - 16) =
___________________________________________________________________________
___________________________________________________________________________
3. Schreibe die Fachbegriffe auf:
a) 45 + 56 = 101
___________________________________________________________________________
b) 71 - 56 = 15
___________________________________________________________________________
c) Term ?
___________________________________________________________________________
d) Formuliere das Assoziativgesetz der Multiplikation im Wortlaut
___________________________________________________________________________
e) Formuliere das Distributivgesetz
___________________________________________________________________________
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 3
1. Stelle den Term auf und rechne !
Dividiere den Wert der Differenz aus 720 und 240 durch den Wert des
Produkts aus 6 und 20!
________________________________________________________________________________________
________________________________________________________________________________________
2. Schreibe jeweils als einen Term (Aufgabe mit Platzhalter). Rechne dann aus!
a) Der Subtrahend heißt 21. Die Differenz ist 9. Wie heißt der Minuend?
_________________________________________________________________
_________________________________________________________________
b) Addiere die Zahl 78 zur Differenz von 71 und 49
__________________________________________________________________
__________________________________________________________________
c) Der erste Summand heißt 42.
Der zweite ist halb so groß wie der erste Summand.
Der dritte Summand ist doppelt so groß wie der zweite
Summand. Wie heißt die Summe?
________________________________________________________
___________________________________________________________________
3. Bilde jeweils den Term zur Angabe. Der Term soll nicht berechnet werden !
a.) Vergrößere die Summe aus den drei kleinsten Quadratzahlen um die
Differenz aus 199 und – 99 ! 199 ist dabei der Minuend !
_________________________________________________________________
_________________________________________________________________
b.) Subtrahiere die Differenz mit dem Subtrahenden 55 und dem
Minuenden – 88 von der Summe aus 912 und der Gegenzahl von 13 !
_________________________________________________________________
_________________________________________________________________
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 4
1. Berechne :
a) 3547 + 29 + 431 + 79 + 5 =
b) 4265 – 156 – 2348 – 8 =
2. Berechne den Term :
a) ( 89 + 52 ) – ( 226 – 159 ) =
b) 76 – 37 + ( 82 – 56 + 41 ) =
c) 390 – [ 273 + ( 64 – 28 )] =
3. Anfang Oktober hatte Familie Winter einen Vorrat von 3290 Liter Heizöl im
Tank. Es wurden dann im Oktober 514 Liter , im November 652 Liter, im
Dezember 874 Liter, im Januar 710 Liter und im Februar 491 Liter
verbraucht.
Stelle einen Term auf, und berechne den Tankinhalt Ende Dezember.
__________________________________________________________________
__________________________________________________________________
4. Herr •aver hat ein 50 m langes Kabel gekauft. Er benötigt 87 dm für
das Wohnzimmer,
12,25 m für die Garage und 9 m 80 cm für die Zimmer im 1. Stock.
Wie viel Kabel hat er noch übrig ?
Stelle einen Term auf !
__________________________________________________________________
5. Stelle nur den Term auf !
a) Addiere zur Differenz der Zahl 69 und 34 die Summe
der Zahlen 78 und 23.
b) Subtrahiere die Differenz der Zahlen 78 und 33 von der Summe der
Zahlen 172 und 43
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 5
1. Stelle den Term auf (nicht berechnen!).
Subtrahiere die Gegenzahl von (– 25 + 17) von der Summe der
Zahlen – 32 und – 18.
_______________________________________________________________
2. Berechne den Wert des Terms in einer fortlaufenden Rechnung.
– 123 + [– 312 – (–213 – 132) + (231 – 321)] =
_______________________________________________________________
3. Berechne folgenden Term:
400 – {298 – [294 – (1237 – 1199)]} + 651 =
_______________________________________________________________
4. Schreibe zu dem folgenden Satz den Term auf, ohne seinen Wert zu
berechnen!
„Subtrahiere die Summe der Zahlen 305 und 678 von der Differenz der
Zahlen 4567 und 543“
_______________________________________________________________
5. Wie ändert sich der Wert einer Summe, wenn beide Summanden um 20
verkleinert werden?
________________________________________________________________
6. Wie ändert sich der Wert einer Differenz, wenn der Minuend um 17
verkleinert und der Subtrahend um 17 vergrößert wird?
__________________________________________________________________
7. Wie ändert sich der Wert der Differenz, wenn man den Minuenden um 4
verkleinert und den Subtrahenden um 6 vergrößert?
Rechnung 1 Ergebnisrechnung
__________
Rechnung 2
Antwort:_________________________________________________
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 6
1. Dividiert man zwei Zahlen, so nennt man das Ergebnis_______ _____________
2. Berechne schrittweise. Notiere die Berechnung korrekt.
a) 784 – 84 : 8 • 3 = ________________________________________________________
b) 17 + 3 • (17 + 23) = ______________________________________________________
c) 294 - [144 – (120 – 24) : 3] = _______________________________________________
3. Notiere den zugehörigen Rechenbaum.
(213 – 17 + 34) • 4 =
4. Schreibe als Term, berechne dann.
a) Dividiere die Differenz der Zahlen 98 und 56 durch den Quotienten der
Zahlen 42 und 7.
__________________________________________________________________________
b) Subtrahiere von der Zahl 99 das Produkt aus der Zahl 6 und der Summe der
Zahlen 5 und 4.
__________________________________________________________________________
5. Rechne vorteilhaft. Du darfst Zwischenschritte aufschreiben. Achte auf den
richtigen Gebrauch des Gleichheitszeichens.
a) 2 • 4 • 17 • 5 • 25 = _____________________________________________________
b) (360 + 18) : 18 = ________________________________________________________
c) 12 • 73 + 8 • 12 – 31 • 12 = _______________________________________________
6. Berechne schriftlich. Wähle eine günstige Reihenfolge. Mache zunächst
einen Überschlag.
a) 9003 • 568 = b) 777 • 948 =
7. Berechne schriftlich.
a) 4844 : 7 = b) 13475 : 49 =
8. Berechne:
a) • = (32178 — 3918) — (489 + 8987) =
b) • = 8 – 8 : 2+23 : 4 =
c) Subtrahiere das Produkt aus 498 und 8 von der Differenz der Zahlen
14440 und 68. (Vergiss den Term nicht.)
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 7
1. Fasse in Worte! (Du brauchst den Term nicht auszurechnen.)
17 + 35 : 5 + 4 7 • 41
__________________________________________________________________________
2. Stelle den Term auf und berechne ihn.
a) Addiere die Summe von -35 und 78 zur Differenz der Gegenzahlen
von 83 und -234.
____________________________________________________________________
b) Subtrahiere das Produkt der Zahlen 7 und 8 vom Quotienten der Zahlen
84 und 21
______________________________________________________________________
3. Wie ändert sich der Wert des Quotienten, wenn man den Divisor
verdoppelt?
________________________________________________________________________
4. Berechne :
a) [+ 15 - |- 9 |- |25 |- 15 -|33 – 78 |] = ____________________________________
___________________________________________________________________________
b) ( 27 • 235 – 63648 : 16) : [14 • 8 – (28 • 4 – 9) ] = ___________________________
___________________________________________________________________________
5. Berechne auf zwei verschiedene Arten :
(161 + 189) : 7 = ____________________________________________________________
___________________________________________________________________________
6. Berechne die Terme. Es wird leichter, wenn Du auf Rechenvorteile achtest.
a) 78 + 642 + 358 + 30 + 122 + 78 = _____________________________________
_________________________________________________________________________
b) 4200 - (400 + 200) - (175 - 75) = _________________________________________
__________________________________________________________________________
7. Berechne schriftlich!
a) 78 + 301 + 55 b) 1253 - 456 - 123 c) 523 • 17 d) 425 : 17
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 8
1. Terme
a) Subtrahiere von der Summe der Summanden 567 und 233 das Produkt der
Faktoren 12 und 8
__________________________________________________________________________
b) Multipliziere den Quotienten der Zahlen 121 und 11 mit der Differenz der
Zahlen 49 und 7.
__________________________________________________________________________
2. Distributivgesetz
Wende bei jeder Aufgabe mindestens einmal sinnvoll das Distributivgesetz an.
a) 125 • 147 - 125 • 139 = b) 60 : 19 + 16 : 19 =
c) 104 • 15 = d) 14 • 21 + 7 • 9 =
3. Berechne die Terme schrittweise und schreibe alle Zwischenschritte auf:
a) 100 + 20 : 4 + 3 =
b) 3 • 24 + (5+3²) =
c) 62 –{5 •[(36 : 6 + 6)]+ 72 : 18} =
4.
a) Mache einen Gesamtansatz und berechne dann die Summe: Addiere
die Summe der größten und der kleinsten vierstelligen Zahl, in der
die 7 und die 8 jeweils genau vorkommt, zur größten dreistelligen
Zahl, in der die 9 nur einmal vorkommt.
b) Ergänze die fehlenden Ziffern!
356_9
_572
+ 6156_
_________
1_4_20
c) Rechne möglichst vorteilhaft. Gib jeweils an, welches Rechengesetz
du verwendest. Wende pro Schritt nur ein Rechengesetz an.
(174+388) + (126+622)
5. Berechne folgende Terme:
a) 17 + 26 • 14 – 108 : 12 = b) 24 + 8 • 12 - (123 : 3 + 71) =
c) (17 + 5 • 27) : 8 – 65 : 5 = d) (15 + 3 • 17) + [223 – 6 • (17 + 4)] =
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 9
1. Übersetze die Texte in einen Term und berechne diesen anschließend.
a) Multipliziere die Summe von 13 und 23 mit 12. Subtrahiere von dem Ergebnis
die Zahl 28.
b) Multipliziere die Summe von 18 und 36 mit der Differenz von 26 und 14.
c) Dividiere die Summe von 36 und 44 durch 5. Addiere zu dem Quotienten
das Produkt aus 6 und 5.
2. Schreibe den Rechenausdruck in Worten und berechne ihn:
(32 + 54) • (48 - 27) =
3. Ein Installateur repariert in der Wohnung der Familie Moritz eine undichte
Wasserleitung. Er verlang für die Anfahrt 22 € und für jede Arbeitsstunde 29 €.
a) Schreibe einen Term, wenn die Reparatur 3 Stunden dauert und berechne
ihn.
b) Der Installateur verlangt 167 €. Wie lange hat die Reparatur gedauert ?
4. Achtung: Bei beiden Aufgabenteilen musst du ausnahmsweise keine
Rechnung aufschreiben, wenn du es ohne hinbekommst.
a) Aus Zahlen, Rechenzeichen und Klammern werden verschiedene Terme
gebastelt. Ordne die Terme nach der Größe ihrer Ergebnisse, beginne mit
dem kleinsten.
17 • 3 + 21, 21 • 3+ 17, 17 • 21 + 3, (17 + 3) • 21, (21 + 3) • 17
b) Versuche mit den Teilen aus der „Materialkiste“ den Term zu finden, der die
größte Zahl liefert. Verwende jedes Teil nur einmal.
8 , 6, 4, 5, •, +, -, ( )
5. Erstelle zu dem folgenden Term eine Textaufgabe:
(9998 – 9001) – (373 – 427)
Berechne den Termwert
6. Schreibe folgende Zahlen mit Ziffern:
a) Fünfzigmillionenzweiundvierzigtausendacht
b) Vierbilliardensechsmilliardendreizehn
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 10
1. Fülle die folgende Tabelle aus:
2. Runden :
a) Runde auf Hunderter: 2357 89 4638 ≈ _____________________
b) Runde auf Tausender: 99945 505 28485 ≈ __________________________
3. Römische Zahlen :
a) Schreibe in arabischen Ziffern :
CLXVII CMXCIV MCDXLIX = ________________________________
b) Schreibe in römischen Zahlen :
46 984 1848 = _________________________________
4. Wie verändert sich eine Summe, wenn man den 2. Summanden um 47
verkleinert und den 1. Summanden um 25 vergrößert.
________________________________________________________________________
5. Gib die Art des Terms an und berechne seinen Wert: 3 2 ● 2 7 – [9 3 + 7 ● ( 7 8 - 9 4 3 : ( - 4 1 ) ) ] : ( 1 5 4 : 7 + 3 ) = ________
6. Notiere 3 Regeln für die Reihenfolge beim Berechnen von
Rechenausdrücken.
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
Terme erstellen und berechnen 5. Klasse – Gymnasium – Arbeitsblatt 11
1. Berechne
a) 5 · 7 + 3 · 4 = b) 20 + 3 · 4 + 16 =
c) (3 + 4) · 9 – 18 = d) 3 · 6 – 12 : 4
e) 31 – 55 : 11 = f) 36 + [21 - (24 - 17) + 25] - 66 =
2. Setze Klammern, so dass wahre Aussagen entstehen.
a) 3 + 9 · 2 = 24 b) 20 + 40 : 5 = 12
c) 24 – 4 · 5 – 50 : 7 + 3 = 95
3. Fülle die Lücken aus, sodass wahre Aussagen entstehen.
a) 6 · 5 + ___ = 40 b) 24 + 4 · ___ =60 c) 3 ·(18 + ___ = 75
4. Berechne die folgenden Rechenausdrücke. Gib alle Zwischenschritte an.
a) 410 + 90 (122 – 88)
b) 6 500 – 5 (1255 – ( 18 + 19 ) 33 ) + 444
c) Subtrahiere den Quotienten der Zahlen 247 und 13 von der achtfachen
Summe der Zahlen 41 und 59.
5. Berechne mit Hilfe des Assoziativgesetzes und des Kommutativgesetzes.
Achte auf Rechenvorteile !
247 + 481 + 353 + 19 + 198 = __________________________________________
______________________________________________________________________
6. Berechne. Wie heißt der Term?
a.) [93 + (52 – 43)] – 86 + [52 – (43 – 5)] = _________________________________
________________________________________________________________________
Name des Terms: _______________________________________________________
b.) 6483 – [893 + (3609 –70)] = ___________________________________________
________________________________________________________________________
Name des Terms: _______________
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 1 1. Berechne folgenden Term !
[(-8) • (-9) + (-54) : 9] • 10 – 2 • 112=
[72 – 54 : 9] • 10 – 2 • 121 =
[72 -6] • 10 – 242 =
66 • 10 -242 =
660 – 242 = 418
2. Berechne !
a. 10 + ( 51 - 3 · 5 ) : 4 = 19 b. 50 - 5 · 7 = 15
c. 100 - ( 16 + 3 · 8 ) + 4 · 12 = 108 d. [ 18 + ( 3 · 12 - 6 · 5 ) ] · 8 = 192
3. Setze in den Gleichungen die Klammern, so dass die angegebenen Ereignisse richtig sind !
a. ( 16 + 14 ) · 2 = 60 b. [ 10 · ( 7 – 2 ) ] + 3 = 53
4. Eine Klasse mit 27 Schülerinnen und Schülern fährt zur Eisenbahn. Die Lehrerin sammelt von jedem
12 € ein. Sie bezahlt für die Schülergruppe insgesamt 287,55 €.
Wie viel Geld bekommt jedes Kind zurück ? Schreibe einen Term oder rechne in einzelnen Schritten!
a. 7 · 12 € = 324 €
b. 324 € -287,55 € = 36,45 €
c. 36,45 € : 27 = 1,35 €
d. Jeder Schüler erhält 1,35 € zurück.
5. Schreibe als Term und berechne dann !
a) Multipliziere die Summe aus 12 und 19 mit der Differenz der Zahlen 444 und 435.
(12 + 19) · (444 – 435) = 31 · 9 = 279
b) Dividiere das Produkt der Zahlen 4 und 14 durch die Differenz der Zahlen 166 und 159.
(4 · 14) : (166 – 139) = 4 · 14 : 7 = 56 : 7 = 8
6. Schreibe zuerst die Aufgabe ins Heft und berechne dann
a) Der Minuend ist 156, der Subtrahend 92. Wie heißt das Ergebnis ? 156-92=64
b) Berechne den Quotienten von 102 und 17. 102:17=6
c) Berechne das Produkt von 36 und 3. 36·3=12
d) Durch welche Zahl muss man 180 dividieren, um 36 zu erhalten ? 180:36=5
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 2
1. Stelle den zugehörigen Rechenterm auf und berechne:
a) Addiere zur Summe der Zahlen 150 und 75 deren Differenz!
(150 + 75( + (150 - 75) = 300
b) Subtrahiere von der Differenz der Zahlen 283 und 156 die Summe der Zahlen 37 und 78
(283 - 156) - (37 + 78 )= 127 – 115 = 12
c) Subtrahiere die Differenz von178 und 94 von der Summe aus 248 und 132
(248 + 132) - (178 - 94) = 380 - 84 = 296
d) Subtrahiere die Differenz der Zahlen 37 und 28 von deren Summe
(37 + 28)-(37 - 28)= 65 - 9 = 56
2. Berechne und gib die Aufgabe in Wortform an!
a) (99 + 15) - (33 - 19) = (99 + 15) - (33 - 19) = 100
Subtrahiere von der Summe aus 99 und 15 die Differenz der Zahlen 33 und 19
b) (82 - 19) - 18 = 45
Subtrahiere von der Differenz der Zahlen 82 und 19 die Zahl 18
c) 100 - (82 - 19 ) = 37
Subtrahiere die Differenz der Zahlen 82 und 19 von der Zahl100
d) (12 + 18) - (28 - 16) = 18
Subtrahiere von der Summe der Zahlen 12 und 18 die Differenz der Zahlen 28 und 16
3. Schreibe die Fachbegriffe auf:
a) 45 + 56 = 101
1.Sumand + 2.Sumand = Summe
b) 71 - 56 = 15
Minuend – Subtrahend = Differenz
c) Term ?
Ein Term ist ein mit Zahlen und Symbolen dargestellter Rechenweg
d) Formuliere das Assoziativgesetz der Multiplikation im Wortlaut
In Summen / Produkten dürfen die Summanden / Faktoren vertauscht werden.
e) Formuliere das Distributivgesetz
3 · [4 + 2 ] = 3 · 4 + 3 · 2 = 12 + 6
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 3
1. Stelle den Term auf und rechne !
Dividiere den Wert der Differenz aus 720 und 240 durch den Wert des Produkts aus 6 und 20!
( 720 – 240 ) : ( 6 20 ) =
480 : 120 = 4
2.Schreibe jeweils als einen Term (Aufgabe mit Platzhalter). Rechne dann aus!
a) Der Subtrahend heißt 21. Die Differenz ist 9. Wie heißt der Minuend?
[] -21 = 9 9 + 21 = [] [] = 30 auch richtig [30] – 21 = 9
Der Minuend ist 30
b) Addiere die Zahl 78 zur Differenz von 71 und 49
(71 — 49) + 78 = 22 + 78 = 100
c) Der erste Summand heißt 42.
Der zweite ist halb so groß wie der erste Summand.
Der dritte Summand ist doppelt so groß wie der zweite Summand.
Wie heißt die Summe?
42 + 21+ 42 = 105 Die Summe ist 105
3. Bilde jeweils den Term zur Angabe. Der Term soll nicht berechnet werden !
a.) Vergrößere die Summe aus den drei kleinsten Quadratzahlen um die Differenz aus 199 und – 99 !
199 ist dabei der Minuend !
( 1 + 4 + 9 )+ [ 199 – (– 99 ) ]
b.) Subtrahiere die Differenz mit dem Subtrahenden 55 und dem Minuenden – 88 von der Summe aus
912 und der Gegenzahl von 13 !
[ 912 + (– 13 ) ] – (– 88 – 55 )
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 4
1. Berechne :
a) 3547 + 29 + 431 + 79 + 5 = 6291
b) 4265 – 156 – 2348 – 8 = 1681
2. Berechne den Term :
a. ( 89 + 52 ) – ( 226 – 15) = 141 – 67 = 74
b. 76 – 37 + ( 82 – 56 + 41 ) = 39 + 67 = 106
c. 390 – [ 273 + ( 64 – 28 )] = 390 – [ 273+ 36 ] = 390 – 309 = 81
3. Anfang Oktober hatte Familie Winter einen Vorrat von 3290 Liter Heizöl im Tank. Es
Wurden dann im Oktober 514 Liter , im November 652 Liter, im Dezember 874 Liter,
im Januar 710 Liter und im Februar 491 Liter verbraucht.
Stelle einen Term auf, und berechne den Tankinhalt Ende Dezember.
3290 – ( 574 + 652 + 514 ) = 3290 – 2040 = 1250
Ende Dezember haben sie noch 1250 Liter Heizöl im Tank
4. Herr •aver hat ein 50 m langes Kabel gekauft. Er benötigt 87 dm für das Wohnzimmer,
12,25 m für die Garage und 9 m 80 cm für die Zimmer im 1. Stock.
Wie viel Kabel hat er noch übrig? Er hat noch 19,25 m Kabel übrig
Stelle einen Term auf ! 5000 – ( 870 + 1225 + 980) = 1925cm oder 19,25m
5. Stelle nur den Term auf!
a. Addiere zur Differenz der Zahl 69 und 34 die Summer der Zahlen 78 und 23
( 69 – 34) + ( 78 + 23 )
b. Subtrahieren die Differenz der Zahlen 78 und33 von der Summe der Zahlen 172 und 43
( 172 + 43 ) – ( 77 – 33 )
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 5
1. Stelle den Term auf (nicht berechnen!).
Subtrahiere die Gegenzahl von (– 25 + 17) von der Summe der Zahlen – 32 und – 18.
[-32 + (-18)] – [-(-25 + 17)]
2. Berechne den Wert des Terms in einer fortlaufenden Rechnung.
– 123 + [– 312 – (–213 – 132) + (231 – 321)] =
– 123 + [– 312 – (– 345) + (– 90)] =
– 123 + [– 312 + 345 – 90] =
– 123 + [ 33 – 90] =
– 123 + [– 57] =
– 123 – 57 = – 180
3. Berechne folgenden Term:
400 – {298 – [294 – (1237 – 1199)]} + 651 =
= 400 – {298 – [294 – 38]} + 651
= 400 – {298 – 256} + 651
= 400 – 42 + 651
= 358 + 651
= 1009
4. Schreibe zu dem folgenden Satz den Term auf, ohne seinen Wert zu berechnen!
„Subtrahiere die Summe der Zahlen 305 und 678 von der Differenz der Zahlen 4567 und
543“
(4567 – 543) – (305 + 678)
5. Wie ändert sich der Wert einer Summe, wenn beide Summanden um 20 verkleinert werden?
Der Wert der Summe verkleinert sich um 40.
6. Wie ändert sich der Wert einer Differenz, wenn der Minuend um 17 verkleinert und der
Subtrahend um 17 vergrößert wird?
Der Wert der Differenz verkleinert sich um 34
7. Wie ändert sich der Wert der Differenz, wenn man den Minuenden um 4
verkleinert und den Subtrahenden um 6 vergrößert?
Rechnung 1 25 – 10 = 15 Ergebnisrechnung 15 – 5 = 10
Rechnung 2 21 – 16 = 5
Antwort: Der Wert der Differenz sinkt um 10.
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 6
1. Dividiert man zwei Zahlen, so nennt man das Ergebnis Quotient
2. Berechne schrittweise. Notiere die Berechnung korrekt.
2a) 784 – (84 : 7) + 8 • 3 2b) 17 + 3 • (17 + 23)
= 784 – 12 + 24 = 17 + 3 • 40
= 784 – 36 = 17 + 120
= 748 = 137
2c) 294 - [144 – (120 – 24) : 3]
= 294 - [144 – 96 : 3]
= 294 - [144 - 32]
= 294 – 112
= 182
3. Notiere den zugehörigen Rechenbaum.
213 17 34 4
l l__+__l
l 51
l l___ •__l
l 204
l___ - _____l
9
4. Schreibe als Term, berechne dann.
a) Dividiere die Differenz der Zahlen 98 und 56 durch den Quotienten der Zahlen 42 und 7.
(98 – 56) : (42 : 7) = 42 : 6 = 7
b) Subtrahiere von der Zahl 99 das Produkt aus der Zahl 6 und der Summe der Zahlen 5 und 4.
99 – 6 • (5 + 4)= 99 – 6 • 9 = 99 – 54 = 45
5. Rechne vorteilhaft. Du darfst Zwischenschritte aufschreiben. Achte auf den
richtigen Gebrauch des Gleichheitszeichens.
a) 2 • 4 • 17 • 5 • 25 4 b) (360 + 18) : 18 4 c) 12 • 73 + 8 • 12 – 31 • 12
= 4 • 25 • 2 • 5 • 17 = 378 : 18 = 12 • (73 + 8 – 31)
= 100 • 10 • 17 = 21 = 12 • 50
= 1000 • 17 = 600
= 17 000
6. Berechne schriftlich. Wähle eine günstige Reihenfolge. Mache zunächst einen Überschlag.
a) 9003 • 568 = gerundet = 5 400 000 errechnet = 5 113 704
b) 777 • 948 = gerundet = 720 000 errechnet = 736 596
7. Berechne schriftlich.
a) 4844 : 7 = 692
b) 13475 : 49 = 275
8. Berechne:
a. • = 18784
b. • = 6
c. • = ( 14440 - 68) – 498 • 8 = 10388
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 7
1. Fasse in Worte! (Du brauchst den Term nicht auszurechnen.) 17 + 35 : 5 + 4 7 • 41
Bilde die Summe aus dem Quotienten von 35 und 5 und dem Produkt
aus 47 und 41 und addiere 17.
2. Stelle den Term auf und berechne ihn.
a) Addiere die Summe von -35 und 78 zur Differenz der Gegenzahlen
von 83 und -234.
( - 83 – 234) + ( - 35 + 78) =
- 317 + 43 = - 274
b) Subtrahiere das Produkt der Zahlen 7 und 8 vom Quotienten der Zahlen
84 und 21
( 84 : 21) - (7 • 8) =
4 – 56 = - 52
3. Wie ändert sich der Wert des Quotienten, wenn man den Divisor verdoppelt?
Der Quotient wird halbiert
4. Berechne:
a) [+ 15 - |- 9 |- |25 |- 15 -|33 – 78 |]
| + 15 – 9 | - |25 – 15 - | - 45 |
=| 6 - |- |10 – 45 |
= 6 - | - 35 |
= 6 – 35 = - 29
b) ( 27 • 235 – 63648 : 16) : [14 • 8 – (28 • 4 – 9) ]
= ( 6345 – 3978) : [112 – (112 – 9) ]
= 2367 : 9 = - 267
5. Berechne auf zwei verschiedene Arten:
(161 + 189) : 7
350 : 7 = 50
161 : 7 + 189 : 7
= 23 + 27 = 50
6. Berechne die Terme. Es wird leichter, wenn Du auf Rechenvorteile achtest.
a) 78 + 642 + 358 + 30 + 122 + 78 b) 4200 - (400 + 200) - (175 - 75)
= 78 + (642 + 358) + 30 + (122 + 78) = 4200 - 600 - 100
= 78 + 1000 + 30 + 200 = 3500
= 1308
7. Berechne schriftlich!
a) 78 + 301 + 55 b) 1253 - 456 - 123 c) 523 • 17 d) 425 : 17
78 1253 523 • 17 425 : 17 = 25
+ 301 - 456 523 34
+ 55 - 123 3661 85
1 1 1 1 1 _______ 85
_____ ______ = 8891 0
= 434 = 674
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 8
1. Terme
a) Subtrahiere von der Summe der Summanden 567 und 233 das Produkt der Faktoren 12 und 8
(567 + 233) - (12 • 8) = 800 - 96 = 704
b) Multipliziere den Quotienten der Zahlen 121 und 11 mit der Differenz der Zahlen 49 und 7.
(121 : 11) • (49 - 7) = 11 • 42 = 462
2. Distributivgesetz
a) 125 • 147 - 125 • 139 b) 60 : 19 + 16 : 19
= 125 • (147 - 139) = (60 + 16) : 19
= 125 • 8 = 76 : 19
= 1000 = 4
c) 104 • 15 d) 14 • 21 + 7 • 9
= (100 • 15) + (4 • 15) = 7 • 2 • 21 + 7 • 9
= 1500 + 60 = 7 • (2 • 21 + 9)
= 1560 = 7 • (42 + 9)
= 7 • 51
= 357
3. Berechne die Terme schrittweise und schreibe alle Zwischenschritte auf:
a) 100 + 20 : 4 + 3 = 100 + 5 + 3 = 108
b) 3 • 24 + (5 + 3²) = 3 • 16 + (5 + 9) = 48 + 14 = 62
c) 62 - {5• [ (36 : 6 + 6) : 6 ] + 72 : 18}
= 62 - {5• [ (6+6) : 6 ] + 72 : 18}
= 62 - {5• [ 12 : 6 ] + 72 : 18}
= 62 - {5• 2 + 72 : 18}
= 62 - {10 + 4}
= 62 - 14
= 48
4.
a) Mache einen Gesamtansatz und berechne dann die Summe: Addiere
die Summe der größten und der kleinsten vierstelligen Zahl, in der
die 7 und die 8 jeweils genau vorkommt, zur größten dreistelligen
Zahl, in der die 9 nur einmal vorkommt.
(174+388) + (126+622)
988 + (8877 + 7788) = 988 + 16665 = 17653
b) Ergänze die fehlenden Ziffern!
35679
7572
+ 61569
104820
c) Rechne möglichst vorteilhaft. Gib jeweils an, welches Rechengesetz
du verwendest. Wende pro Schritt nur ein Rechengesetz an.
(174 + 388) + (126 + 622)
AG = 174 + 388 + 126 + 622
KG = 174 + 126 + 388 + 622
AG = (174 + 126) + (388 + 622)
= 300 + 1010 = 1310
5. Berechne folgende Terme:
a) 17 + 26 • 14 – 108 : 12 b) 24+812-(123:3+71)
= 17 + 364 - 9 = 24 + 96 -(41 + 71)
= 381 - 9 = 24 + 96 - 112
= 372 = 120 - 112
= 8
c) (17 + 5 • 27) : 8 – 65 : 5 d) (15 + 3 • 17) + [223 – 6 • (17 + 4)]
= (17 + 135) : 8 - 13 = (15 + 51)+(223 – 6 • 21)
= (17 + 135) : 8 - 13 = 66 + (223 – 126)
= 152 : 8 - 13 = 66 + 97
= 19 - 13 = 163
= 6
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 9 1. Übersetze die Te•te in einen Term und berechne diesen anschließend.
a) Multipliziere die Summe von 13 und 23 mit 12. Subtrahiere von dem Ergebnis die Zahl 28.
(13 + 23) • 12 -28
= 36 • 12 - 28
= 432 - 28
= 404
b) Multipliziere die Summe von 18 und 36 mit der Differenz von 26 und 14.
(18 + 36) • (26 - 14)
=54 • 12
=648
c) Dividiere die Summe von 36 und 44 durch 5. Addiere zu dem Quotienten das Produkt aus 6 und 5.
(36 + 44) : 5 +6 • 5
=80 : 5 + 30
=16 + 30
=46
2. Schreibe den Rechenausdruck in Worten und berechne ihn:
(32 + 54) • (48 - 27) = 86 • 21 = 806
Multipliziere die Summe von 32 und 54 mit der Differenz von 48 und 27
3. Ein Installateur repariert in der Wohnung der Familie Moritz eine undichte
Wasserleitung. Er verlang für die Anfahrt 22 € und für jede Arbeitsstunde 29 €.
a) Schreibe einen Term, wenn die Reparatur 3 Stunden dauert und berechne ihn.
R: 29 • 3 + 22 = 87 + 22 = 109
A: Es würde 109 € kosten.
b) Der Installateur verlangt 167 €. Wie lange hat die Reparatur gedauert ?
R: (167 - 22) : 29 = 145 : 29 = 5
A: Die Reparatur hat 5 Stunden gedauert.
4. Achtung: Bei beiden Aufgabenteilen musst du ausnahmsweise keine Rechnung aufschreiben,
wenn du es ohne hinbekommst.
a) Aus Zahlen, Rechenzeichen und Klammern werden verschiedene Terme
gebastelt. Ordne die Terme nach der Größe ihrer Ergebnisse, beginne mit dem kleinsten.
17 • 3 + 21, 21 • 3+ 17, 17 • 21 + 3, (17 + 3) • 21, (21 + 3) • 17
17•3+21<21•3+17<17•21+3<(21+3)•17<(17+3)•21
b) Versuche mit den Teilen aus der „Materialkiste“ den Term zu finden, der die
größte Zahl liefert. Verwende jedes Teil nur einmal. 8 , 6, 4, 5, •, +, -, ( )
(6 + 5) • 8 – 4 = 84
5. Erstelle zu dem folgenden Term eine Textaufgabe:
(9998 – 9001) – (373 – 427)
Berechne den Termwert
Dividiere die Summe der Zahlen 373 und 427 von der Differenz der
Zahlen 9998 und 9001.
(9998 – 9001) - (373 + 427) =
997 - 800 = 197
6. Schreibe folgende Zahlen mit Ziffern:
a) Fünfzigmillionenzweiundvierzigtausendacht 50 042 008
b) Vierbilliardensechsmilliardendreizehn 4 000 006 000 000 013
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 10
1. Fülle die folgende Tabelle aus:
2. Runden :
a) Runde auf Hunderter: 2357; 89; 4638; ≈ 2400, 100, 4600
b) Runde auf Tausender: 99945 505 28485 ≈ 100 000, 1 000, 28 000
3. Römische Zahlen :
a) Schreibe in arabischen Ziffern :
CLXVII, CMXCIV, MCDXLIX = 167, 994, 1449
b) Schreibe in römischen Zahlen :
46, 984, 1848 = XLVI, CMLXXXIV, MOCCCXLVIII
4. Wie verändert sich eine Summe, wenn man den 2. Summanden um 47 verkleinert und den 1.
Summanden um 25 vergrößert.Der Wert wird um 47 – 25 = 22 kleiner
Beisp. 50+ 50 = 100
75 + 3 = 78 daraus ergibt sich 100 – 78 = 22
5. Gib die Art des Terms an und berechne seinen Wert:
Der Term ist eine Differenz, der Wert beträgt 832.
3 2 ● 2 7 – [ 9 3 + 7 ● ( 7 8 - 9 4 3 : ( - 4 1 ) ) ] : ( 1 5 4 : 7 + 3 ) =
( 3 2 ● 2 7 ) – [ 9 3 + 7 ● ( 7 8 – { 9 4 3 : ( - 4 1 ) } ) ] : [ ( 1 5 4 : 7 ) + 3 ] =
( 8 6 4 ) – [ 9 3 + 7 ● ( 7 8 – { - 2 3 } ) ] : [ ( 2 2 ) + 3 ] =
( 8 6 4 ) – [ 9 3 + 7 ● ( 1 0 1 ) ] : [ 2 5 ] =
( 8 6 4 ) – [ 9 3 + 7 0 7 ] : [ 2 5 ] =
( 8 6 4 ) – [ 8 0 0 ] : [ 2 5 ] =
( 8 6 4 ) – [ 3 2 ] = 8 3 2
6. Notiere 3 Regeln für die Reihenfolge beim Berechnen von Rechenausdrücken.
Punkt vor Strich
Klammern zuerst rechnen
Innere Klammern zuerst rechnen
Terme erstellen und berechnen 5. Klasse – Lösungen – Arbeitsblatt 11 1. Berechne
a) 5 · 7 + 3 · 4 = 47 b) 20 + 3 · 4 + 16 =48 c) (3 + 4) · 9 – 18 = 45
d) 3 · 6 – 12 : 4= 15 e) 31 – 55 : 11=26 f) 36 + [21 - ( 24 - 17) + 25] – 66 = 9
2. Setze Klammern, so dass wahre Aussagen entstehen.
a) (3 + 9) · 2 = 24 b) (20 + 40) : 5 = 12
c) (24 – 4) · 5 – [50 : (7 + 3)] = 95
3. Fülle die Lücken aus, sodass wahre Aussagen entstehen.
a) 6 · 5 + _10_ = 40 b) 24 + 4 · _9_ = 60 c) 3 ·(18 + _7_) = 75
4. Berechne die folgenden Rechenausdrücke. Gib alle Zwischenschritte an.
a) 410 + 90 (122 – 88 )
= 410 + 90 34
= 410 + 3 060
= 3 470
b) 6 500 – 5 [ 1 225 – ( 18 + 19 ) 33 ]+ 444
= 6 500 – 5 [ 1 225 – 37 33 ] + 444
= 6 500 – 5 [ 1 225 – 1210 ] + 444
= 6 500 – 5 15 + 444
= 6 500 – 75 + 444
= 6 425 + 444
= 6 869
c) 8 (41+59) – (247 : 13 )
= 8 100 – 19
= 800 – 19
= 781
5. Berechne mit Hilfe des Assoziativgesetzes und des Kommutativgesetzes. Achte auf
Rechenvorteile !
247 + 481 + 353 + 19 + 198 = (247+353) + (481+19) + 193 = 600 + 500 +198 = 1298
6. Berechne. Wie heißt der Term?
a.) [93 + (52 – 43)] – 86 + [52 – (43 – 5)] = [93+9] – 86 + [52-38] = 102 – 86 +14 = 16 + 14 = 30
Name des Terms: Summe
b.) 6483 – [893 + (3609 –70)] = 6483 – [893 + 3539] = 6483 – 4432 = 2051
Name des Terms: Differenz