Mathematik Klassenarbeit Nr. 1 Name: __________________________________ Klasse 10a Punkte: ____ / 22 Note: ________ erste mündliche Note: ____
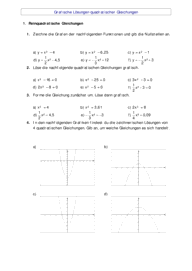
Aufgabe 1: (3 Punkte) Löse die Gleichung.
Aufgabe 2: (3 Punkte) Löse das Gleichungssystem. Gib die Lösungsmenge an. (1) (2)
Aufgabe 3: (3 Punkte) Gib die Definitionsmenge und die Lösungsmenge der Gleichung an.
Aufgabe 4: (3 Punkte) Eine nach unten geöffnete Parabel p1 hat die Gleichung . Eine nach oben geöffnete Normalparabel p2 hat den Scheitelpunkt S2(5|-6). Berechne die Koordinaten der Schnittpunkte der beiden Parabeln.
Aufgabe 5: (5,5 Punkte) Eine nach oben geöffnete Normalparabel und eine Gerade g haben die Punkte A(0|5) und B(-5,5|2,25) gemeinsam.
Berechne die Gleichung der zu g parallelen Geraden, die durch den Scheitelpunkt der Parabel
verläuft.
Aufgabe 6: (4,5 Punkte) Eine nach oben geöffnete Normalparabel hat den Scheitelpunkt S(4|-9). Die Schnittpunkte der Parabel mit der x-Achse werden mit N1 und N2 bezeichnet. N1 und N2 bilden mit einem Punkt P der Parabel ein Dreieck. Berechne den Flächeninhalt des Dreiecks für P(1,5|yP). P bewegt sich jetzt auf der Parabel unterhalb der x-Achse.
Wie groß kann der Flächeninhalt des Dreiecks N1N2P höchstens werden?
Mathematik Klassenarbeit Nr. 1 Name: __________________________________ Klasse 10a Punkte: ____ / 22 Note: ________ erste mündliche Note: ____
Aufgabe 1: (3 Punkte) Löse die Gleichung.
Lösungsformel: ; L={-2;0,5}
Aufgabe 2: (3 Punkte) Löse das Gleichungssystem. Gib die Lösungsmenge an. (3) (1 ́) 5y-3x =-15 (4) (2`) 2x+ x =-17 (2`) multipliziert mit 3: 6y+3x=-51 (1`)+(2 ́ ́): 11y =-66 y=-6 y in (1`) eingesetzt: -30-3x=-15 x=-5
L={(-5|-6)}
Aufgabe 3: (3 Punkte) Gib die Definitionsmenge und die Lösungsmenge der Gleichung an.
D = R \{-2;2}; Hauptnenner: 3(x-2)(x+2)
Nach der Multiplikation mit dem Hauptnenner: Nach Beseitigung der Klammern und zusammenfassen: Umstellung in Normalform: Einsetzen in die Lösungsformel:
Aufgabe 4: (3 Punkte) Eine nach unten geöffnete Parabel p1 hat die Gleichung . Eine nach oben geöffnete Normalparabel p2 hat den Scheitelpunkt S2(5|-6). Berechne die Koordinaten der Schnittpunkte der beiden Parabeln. p2: y=(x-5)²-6 y=x²-10x+19 p1 und p2 gleichsetzen: Einsetzen in die Lösungsformel:
Jeweils in die angegebenen Gleichungen einsetzen ergibt y=-5 und y=3.
L={(6|-5);(2|3)}
Aufgabe 5: (5,5 Punkte) Eine nach oben geöffnete Normalparabel und eine Gerade g haben die Punkte A(0|5) und B(-5,5|2,25) gemeinsam. Berechne die Gleichung der zu g parallelen Geraden, die durch den Scheitelpunkt der Parabel
verläuft. Bestimmung der Parabelfunktion mithilfe eines Gleichungssystems: (1) (2) Normalform: Scheitelform durch quadratische Ergänzung: Scheitelpunkt: S(3|-4) Bestimmung der Geradenfunktion mithilfe der Steigung: Einsetzen des Parabelscheitelpunkts: Gleichung der parallelen Gerade:
Aufgabe 6: (4,5 Punkte) Eine nach oben geöffnete Normalparabel hat den Scheitelpunkt S(4|-9). Die Schnittpunkte der Parabel mit der x-Achse werden mit N1 und N2 bezeichnet. N1 und N2 bilden mit einem Punkt P der Parabel ein Dreieck. Berechne den Flächeninhalt des Dreiecks für P(1,5|yP). Scheitelform: Nullstellenberechnung der Parabel: Punkt P Berechnung durch einsetzen der x-Koordinate:
Flächeninhaltsberechnung mit
Abstand der beiden Nullstellen als Basis des Dreiecks: 7-1=6
Höhe des Dreiecks mit Abstand zwischen P und der x-Achse: 2,75 P bewegt sich jetzt auf der Parabel unterhalb der x-Achse. Wie groß kann der Flächeninhalt des Dreiecks N1N2P höchstens werden?
Punkt P kann den maximalen Abstand des Scheitelpunktes haben, also P=S: Flächeninhaltsberechnung mit
Höhe des Dreiecks mit Abstand zwischen S und der x-Achse: 9 www.klassenarbeiten.de