www.klassenarbeiten.de Seite 1
Vorbereitung auf den Hauptschulabschluss – Übung 1
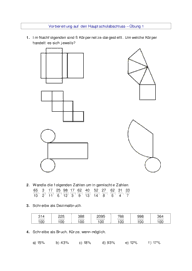
1. Im Nachfolgenden sind 5 Körpernetze dargestellt. Um welche Körper
handelt es sich jeweils?
2. Wandle die folgenden Zahlen um in gemischte Zahlen.
65 3 17 25 98 17 62 40 52 27 62 31 33; ; ; ; ; ; ; ; ; ; ; ; 10 2 11 6 12 3 9 13 14 8 5 4 7
Schreibe als Dezimalbruch.3.
314
100
225
100
388
100
2095
100
766
100
998
100
364
100
Schreibe als Bruch. Kürze, wenn möglich.4.
a) 15% b) 43% c) 18% d) 93% e) 12% f) 17%
Vorbereitung auf den Hauptschulabschluss – Übung 1
1. Im Nachfolgenden sind 5 Körpernetze dargestellt. Um welche Körper
handelt es sich jeweils?
2. Wandle die folgenden Zahlen um in gemischte Zahlen.
65 3 17 25 98 17 62 40 52 27 62 31 33; ; ; ; ; ; ; ; ; ; ; ; 10 2 11 6 12 3 9 13 14 8 5 4 7
Schreibe als Dezimalbruch.3.
314
100
225
100
388
100
2095
100
766
100
998
100
364
100
Schreibe als Bruch. Kürze, wenn möglich.4.
a) 15% b) 43% c) 18% d) 93% e) 12% f) 17%
www.klassenarbeiten.de Seite 2
5. Nach einer Mieterhöhung von 6% muss Frau Schneider 24 € mehr Miete
zahlen. Berechne die Höhe der alten und der neuen Miete.
Schreibe als Bruch. Kürze, wenn möglich.6.
a) 15% b) 43% c) 18% d) 93% e) 12% f) 17%
Löse die folgenden Gleichungen.
a) 4x – 2 = 0 b) 3x + 5 = 2x + 10
7.
1c) 5 x 22− = 1 x d) 15 5 + =
8. Eine dreieckige Zeltbahn ist 3,40 m breit und 1,90 m hoch. Wie viel Stoff
benötigt man für 4 Zeltbahnen?
9. Konstruiere ein Dreieck mit der Grundseite c = 8 cm und der Seite b = 6
cm. Der Winkel α soll 55° groß sein. Trage die Höhe hc ein und berechne
den Flächeninhalt des Dreiecks.
4,9 cm
8,0 cm
6,0 cm
55,0 °
c
ab
A B
C
5. Nach einer Mieterhöhung von 6% muss Frau Schneider 24 € mehr Miete
zahlen. Berechne die Höhe der alten und der neuen Miete.
Schreibe als Bruch. Kürze, wenn möglich.6.
a) 15% b) 43% c) 18% d) 93% e) 12% f) 17%
Löse die folgenden Gleichungen.
a) 4x – 2 = 0 b) 3x + 5 = 2x + 10
7.
1c) 5 x 22− = 1 x d) 15 5 + =
8. Eine dreieckige Zeltbahn ist 3,40 m breit und 1,90 m hoch. Wie viel Stoff
benötigt man für 4 Zeltbahnen?
9. Konstruiere ein Dreieck mit der Grundseite c = 8 cm und der Seite b = 6
cm. Der Winkel α soll 55° groß sein. Trage die Höhe hc ein und berechne
den Flächeninhalt des Dreiecks.
4,9 cm
8,0 cm
6,0 cm
55,0 °
c
ab
A B
C
www.klassenarbeiten.de Seite 3
Vorbereitung auf den Hauptschulabschluss – Weitere Übungen
Berechne die folgenden Produkte:1.
1 3 a) 2 5 ⋅ 8 9 b) 9 4 ⋅ 7 4 c) 8 7 ⋅ 8 35 d) 21 24⋅ 3 2 e) 5 7 ⋅
Berechne.
a) 244,66 + 3425,221 – 16,855 b) 3428,28 – 164,441 + 199,6
c) 3441,099 + 11,866 – 12,226 d) 155,44 – 2,68 + 13,688
2.
e) 777,031 – 444,29 + 713,66 f) 444,499 + 500,2 – 216,84
Her Meister hat sein altes Auto verkauft. Ein Verkäufer im Autohaus
unterbreitet ihm für den Kauf eines Neuwagens zum Preis von 21000 €
folgende Angebote:
Angebot 1
Anzahl 40% des Kaufpreises und
36 Monatsraten zu je
360 €.
Angebot 2
Anzahlung 30% des Kaufpreises und
60 Monatsraten zu je
270 €.
3.
Welches Angebot ist günstiger? Begründe deine Entscheidung.
Um wie viel Prozent wird das Auto bei der von dir gewählten Finanzierung
teurer als der Kaufpreis von 21000 €?
Berechne die fehlenden Werte.
Prozentsatz Prozentwert Grundwert
20% 240 €
5% 350 €
63,00 € 252 €
88,00 € 220 €
14% 56,00 €
4.
7% 24,50 €
5. Ein Landwirt hat einen Grundbesitz von 5400 a. Der Boden wird zu 54% als
Ackerland und zu 34% als Weideland genutzt. Der Rest ist Waldbestand.
Wie groß sind die jeweiligen Flächen?
6. Ein PKW benötigt für 100 km 6,8 Liter Kraftstoff.
a) a) Wie viel Liter Kraftstoff muss man für eine Fahrstrecke von 1
200 km mindestens einplanen?
b) b) Der Tank fasst 43 Liter. Wie viel Kilometer kann man bei
diesem Kraftstoffverbrauch mit einer Tankfüllung maximal fahren?
Vorbereitung auf den Hauptschulabschluss – Weitere Übungen
Berechne die folgenden Produkte:1.
1 3 a) 2 5 ⋅ 8 9 b) 9 4 ⋅ 7 4 c) 8 7 ⋅ 8 35 d) 21 24⋅ 3 2 e) 5 7 ⋅
Berechne.
a) 244,66 + 3425,221 – 16,855 b) 3428,28 – 164,441 + 199,6
c) 3441,099 + 11,866 – 12,226 d) 155,44 – 2,68 + 13,688
2.
e) 777,031 – 444,29 + 713,66 f) 444,499 + 500,2 – 216,84
Her Meister hat sein altes Auto verkauft. Ein Verkäufer im Autohaus
unterbreitet ihm für den Kauf eines Neuwagens zum Preis von 21000 €
folgende Angebote:
Angebot 1
Anzahl 40% des Kaufpreises und
36 Monatsraten zu je
360 €.
Angebot 2
Anzahlung 30% des Kaufpreises und
60 Monatsraten zu je
270 €.
3.
Welches Angebot ist günstiger? Begründe deine Entscheidung.
Um wie viel Prozent wird das Auto bei der von dir gewählten Finanzierung
teurer als der Kaufpreis von 21000 €?
Berechne die fehlenden Werte.
Prozentsatz Prozentwert Grundwert
20% 240 €
5% 350 €
63,00 € 252 €
88,00 € 220 €
14% 56,00 €
4.
7% 24,50 €
5. Ein Landwirt hat einen Grundbesitz von 5400 a. Der Boden wird zu 54% als
Ackerland und zu 34% als Weideland genutzt. Der Rest ist Waldbestand.
Wie groß sind die jeweiligen Flächen?
6. Ein PKW benötigt für 100 km 6,8 Liter Kraftstoff.
a) a) Wie viel Liter Kraftstoff muss man für eine Fahrstrecke von 1
200 km mindestens einplanen?
b) b) Der Tank fasst 43 Liter. Wie viel Kilometer kann man bei
diesem Kraftstoffverbrauch mit einer Tankfüllung maximal fahren?
www.klassenarbeiten.de Seite 4
Löse die Klammern auf.
a) (x + 3)² b) (x – 4)²
7.
c) (2x + 1)² d) (x + 3)(x – 3)
8. Trage die folgenden Punkte in ein rechtwinkliges Koordinatensystem ein:
A(0/0), B(4/–2), C(4/0).
a) a) Zeichne das Dreieck ABC.
b) b) Berechne die Länge der Strecke AB.
9. Ein quaderförmiges Schwimmbecken ist 50 m lang, 25 m breit und 2,60 m
tief.
a) a) Wie viel Kubikmeter Wasser fasst das Becken, wenn es bis zu
20 cm unter dem Beckenrand gefüllt ist?
b) b) Zum Auspumpen des Beckens benutzt man eine Pumpe, die 2
m³ Wasser je Minute fördert. Nach wie viel Stunden ist das Becken
leer?
Löse die Klammern auf.
a) (x + 3)² b) (x – 4)²
7.
c) (2x + 1)² d) (x + 3)(x – 3)
8. Trage die folgenden Punkte in ein rechtwinkliges Koordinatensystem ein:
A(0/0), B(4/–2), C(4/0).
a) a) Zeichne das Dreieck ABC.
b) b) Berechne die Länge der Strecke AB.
9. Ein quaderförmiges Schwimmbecken ist 50 m lang, 25 m breit und 2,60 m
tief.
a) a) Wie viel Kubikmeter Wasser fasst das Becken, wenn es bis zu
20 cm unter dem Beckenrand gefüllt ist?
b) b) Zum Auspumpen des Beckens benutzt man eine Pumpe, die 2
m³ Wasser je Minute fördert. Nach wie viel Stunden ist das Becken
leer?
www.klassenarbeiten.de Seite 5
Vorbereitung auf den Hauptschulabschluss – Übung 1 – Lösungen
1. Im Nachfolgenden sind 5 Körpernetze dargestellt. Um welche Körper
handelt es sich jeweils?
Bei den abgebildeten Netzen handelt es sich um einen Quader, eine
Pyramide, einen Würfel, einen Zylinder und einen Kegel.
2. Wandle die folgenden Zahlen um in gemischte Zahlen.
5 1 6 1 2 2 8 1 10 3 2 3 5 6 ;1 ;1 ; 4 ;8 ;5 ;6 ;3 ;3 ;3 ;12 ;7 ;4 1
65 3 17 25 98 17 62 40 52 27 62 31
0 2 11 6 12 3 9 1
33; ; ; ; ; ; ; ; ; ; ; ; 10 2 11 6 12 3 9 13 14 8 5 4 7
3 14 8 5 4 7
Schreibe als Dezimalbruch.
314
100
225
100
388
100
2095
100
766
100
998
100
364
100
3.
= 3,14 = 2,25 = 3,88 = 20,95 = 7,66 = 9,98 = 3,64
Vorbereitung auf den Hauptschulabschluss – Übung 1 – Lösungen
1. Im Nachfolgenden sind 5 Körpernetze dargestellt. Um welche Körper
handelt es sich jeweils?
Bei den abgebildeten Netzen handelt es sich um einen Quader, eine
Pyramide, einen Würfel, einen Zylinder und einen Kegel.
2. Wandle die folgenden Zahlen um in gemischte Zahlen.
5 1 6 1 2 2 8 1 10 3 2 3 5 6 ;1 ;1 ; 4 ;8 ;5 ;6 ;3 ;3 ;3 ;12 ;7 ;4 1
65 3 17 25 98 17 62 40 52 27 62 31
0 2 11 6 12 3 9 1
33; ; ; ; ; ; ; ; ; ; ; ; 10 2 11 6 12 3 9 13 14 8 5 4 7
3 14 8 5 4 7
Schreibe als Dezimalbruch.
314
100
225
100
388
100
2095
100
766
100
998
100
364
100
3.
= 3,14 = 2,25 = 3,88 = 20,95 = 7,66 = 9,98 = 3,64
www.klassenarbeiten.de Seite 6
Schreibe als Bruch. Kürze, wenn möglich.
a) 15% b) 43% c) 18% d) 93% e) 12% f) 17%
4.
15 3
100 20= = 43
100= 18 9
100 50= = 93
100= 12 3
100 25= = 17
100=
Nach einer Mieterhöhung von 6% muss Frau Schneider 24 € mehr Miete
zahlen. Berechne die Höhe der alten und der neuen Miete.
5.
Gesucht ist der Grundwert.
100G 24 400 €6= ⋅ = – Die alte Miete betrug 400 €, jetzt zahlt sie 424 €.
Schreibe als Bruch. Kürze, wenn möglich.
a) 15% b) 43% c) 18% d) 93% e) 12% f) 17%
6.
15 3
100 20= = 43
100= 18 9
100 50= = 93
100= 12 3
100 25= = 17
100=
Löse die folgenden Gleichungen.
a) 4x – 2 = 0 b) 3x + 5 = 2x + 10
L = { 0,5 } L = { 5 }
1c) 5 x 22− = 1 x d) 15 5 + =
7.
L = { 6 } L = { 4 }
8. Eine dreieckige Zeltbahn ist 3,40 m breit und 1,90 m hoch. Wie viel Stoff
benötigt man für 4 Zeltbahnen?
3, 4 1,9A 4 12,92 m² 2
⋅= ⋅ =
Schreibe als Bruch. Kürze, wenn möglich.
a) 15% b) 43% c) 18% d) 93% e) 12% f) 17%
4.
15 3
100 20= = 43
100= 18 9
100 50= = 93
100= 12 3
100 25= = 17
100=
Nach einer Mieterhöhung von 6% muss Frau Schneider 24 € mehr Miete
zahlen. Berechne die Höhe der alten und der neuen Miete.
5.
Gesucht ist der Grundwert.
100G 24 400 €6= ⋅ = – Die alte Miete betrug 400 €, jetzt zahlt sie 424 €.
Schreibe als Bruch. Kürze, wenn möglich.
a) 15% b) 43% c) 18% d) 93% e) 12% f) 17%
6.
15 3
100 20= = 43
100= 18 9
100 50= = 93
100= 12 3
100 25= = 17
100=
Löse die folgenden Gleichungen.
a) 4x – 2 = 0 b) 3x + 5 = 2x + 10
L = { 0,5 } L = { 5 }
1c) 5 x 22− = 1 x d) 15 5 + =
7.
L = { 6 } L = { 4 }
8. Eine dreieckige Zeltbahn ist 3,40 m breit und 1,90 m hoch. Wie viel Stoff
benötigt man für 4 Zeltbahnen?
3, 4 1,9A 4 12,92 m² 2
⋅= ⋅ =
= 1046,401
www.klassenarbeiten.de Seite 7
9. Konstruiere ein Dreieck mit der Grundseite c = 8 cm und der Seite b = 6
cm. Der Winkel α soll 55° groß sein. Trage die Höhe hc ein und berechne
den Flächeninhalt des Dreiecks.
4,9 cm
8,0 cm
6,0 cm
55,0 °
c
ab
A B
C
Konstruktionsbeschreibung:
1. Es wird die Strecke c mit den Endpunkten A und B gezeichnet.
2. In A wird α angetragen.
3. Um A wird ein Kreisbogen b = 6 cm angetragen, es entsteht C.
4. C und B werden miteinander verbunden.
5. Von C wird das Lot auf c gefällt – die Höhe hc ist 4,9 cm lang.
Für die Fläche ergibt sich:
8 4,9 A 19,6 cm²2
⋅= =
Vorbereitung auf den Hauptschulabschluss – Weitere Übungen – Lösungen
Berechne die folgenden Produkte:1.
1 3 a) 2 5
3
10⋅ = 28 9 b) 9 4 ⋅ = 7 4 ) 8
1c 7 2⋅ = 8 35 d) 21 2
5
4 9⋅ = 3 2 e) 5 7
6
35⋅ =
Berechne.
a) 244,66 + 3425,221 – 16,855 b) 3428,28 – 164,441 + 199,6
= 3653,026 = 3463,439
c) 3441,099 + 11,866 – 12,226 d) 155,44 – 2,68 + 13,688
= 3440,649 = 166,448
e) 777,031 – 444,29 + 713,66 f) 444,499 + 500,2 – 216,84
2.
= 727,859
www.klassenarbeiten.de Seite 7
9. Konstruiere ein Dreieck mit der Grundseite c = 8 cm und der Seite b = 6
cm. Der Winkel α soll 55° groß sein. Trage die Höhe hc ein und berechne
den Flächeninhalt des Dreiecks.
4,9 cm
8,0 cm
6,0 cm
55,0 °
c
ab
A B
C
Konstruktionsbeschreibung:
1. Es wird die Strecke c mit den Endpunkten A und B gezeichnet.
2. In A wird α angetragen.
3. Um A wird ein Kreisbogen b = 6 cm angetragen, es entsteht C.
4. C und B werden miteinander verbunden.
5. Von C wird das Lot auf c gefällt – die Höhe hc ist 4,9 cm lang.
Für die Fläche ergibt sich:
8 4,9 A 19,6 cm²2
⋅= =
Vorbereitung auf den Hauptschulabschluss – Weitere Übungen – Lösungen
Berechne die folgenden Produkte:1.
1 3 a) 2 5
3
10⋅ = 28 9 b) 9 4 ⋅ = 7 4 ) 8
1c 7 2⋅ = 8 35 d) 21 2
5
4 9⋅ = 3 2 e) 5 7
6
35⋅ =
Berechne.
a) 244,66 + 3425,221 – 16,855 b) 3428,28 – 164,441 + 199,6
= 3653,026 = 3463,439
c) 3441,099 + 11,866 – 12,226 d) 155,44 – 2,68 + 13,688
= 3440,649 = 166,448
e) 777,031 – 444,29 + 713,66 f) 444,499 + 500,2 – 216,84
2.
= 727,859
www.klassenarbeiten.de Seite 8
Her Meister hat sein altes Auto verkauft. Ein Verkäufer im Autohaus
unterbreitet ihm für den Kauf eines Neuwagens zum Preis von 21000 €
folgende Angebote:
Angebot 1
Anzahl 40% des Kaufpreises und
36 Monatsraten zu je
360 €.
Angebot 2
Anzahlung 30% des Kaufpreises und
60 Monatsraten zu je
270 €.
3.
Welches Angebot ist günstiger? Begründe deine Entscheidung.
Um wie viel Prozent wird das Auto bei der von dir gewählten Finanzierung
teurer als der Kaufpreis von 21000 €?
Angebot 1:
4021000 36 360 21360 €100⋅ + ⋅ =
Angebot 2:
3021000 60 270 22500 €100⋅ + ⋅ =
Das erste Angebot ist günstiger (Preisvergleich).
Er muss beim 1. Angebot 360 € mehr bezahlen. Das Auto wird damit um
360p% 1,7% teurer.21000= ≈
Berechne die fehlenden Werte.
Prozentsatz Prozentwert Grundwert
20% 48 € 240 €
5% 17,5 € 350 €
25% 63,00 € 252 €
40% 88,00 € 220 €
14% 56,00 € 400 €
4.
7% 24,50 € 350 €
5. Ein Landwirt hat einen Grundbesitz von 5400 a. Der Boden wird zu 54% als
Ackerland und zu 34% als Weideland genutzt. Der Rest ist Waldbestand.
Wie groß sind die jeweiligen Flächen?
54Ac ker land : P 5400 2916 a100
34Weideland : P 5400 1836 a100
12Wald : P 5400 648 a100
= ⋅ =
= ⋅ =
= ⋅ =
Her Meister hat sein altes Auto verkauft. Ein Verkäufer im Autohaus
unterbreitet ihm für den Kauf eines Neuwagens zum Preis von 21000 €
folgende Angebote:
Angebot 1
Anzahl 40% des Kaufpreises und
36 Monatsraten zu je
360 €.
Angebot 2
Anzahlung 30% des Kaufpreises und
60 Monatsraten zu je
270 €.
3.
Welches Angebot ist günstiger? Begründe deine Entscheidung.
Um wie viel Prozent wird das Auto bei der von dir gewählten Finanzierung
teurer als der Kaufpreis von 21000 €?
Angebot 1:
4021000 36 360 21360 €100⋅ + ⋅ =
Angebot 2:
3021000 60 270 22500 €100⋅ + ⋅ =
Das erste Angebot ist günstiger (Preisvergleich).
Er muss beim 1. Angebot 360 € mehr bezahlen. Das Auto wird damit um
360p% 1,7% teurer.21000= ≈
Berechne die fehlenden Werte.
Prozentsatz Prozentwert Grundwert
20% 48 € 240 €
5% 17,5 € 350 €
25% 63,00 € 252 €
40% 88,00 € 220 €
14% 56,00 € 400 €
4.
7% 24,50 € 350 €
5. Ein Landwirt hat einen Grundbesitz von 5400 a. Der Boden wird zu 54% als
Ackerland und zu 34% als Weideland genutzt. Der Rest ist Waldbestand.
Wie groß sind die jeweiligen Flächen?
54Ac ker land : P 5400 2916 a100
34Weideland : P 5400 1836 a100
12Wald : P 5400 648 a100
= ⋅ =
= ⋅ =
= ⋅ =
www.klassenarbeiten.de Seite 9
6. Ein PKW benötigt für 100 km 6,8 Liter Kraftstoff.
c) a) Wie viel Liter Kraftstoff muss man für eine Fahrstrecke von 1
200 km mindestens einplanen?
d) b) Der Tank fasst 43 Liter. Wie viel Kilometer kann man bei
diesem Kraftstoffverbrauch mit einer Tankfüllung maximal fahren?
Lösung a)
Man muss 81,6 Liter einplanen.
Lösung b)
Man schafft ca. 632 km.
Löse die Klammern auf.
a) (x + 3)² = x² + 6x + 9 b) (x – 4)² = x² – 8x + 16
7.
c) (2x + 1)² = 4x² + 4x + 1 d) (x + 3)(x – 3) = x² – 9
8. Trage die folgenden Punkte in ein rechtwinkliges Koordinatensystem ein:
A(0/0), B(4/–2), C(4/0).
c) a) Zeichne das Dreieck ABC.
d) b) Berechne die Länge der Strecke AB.
Lösung a)
A
B
C
-1 1 2 3 4 5
1
-1
-2
Lösung b)
Für die Berechnung wenden wir den „Satz des Pythagoras“ an.
2 2 2
AB AC BC
AB 4² 2²
AB 4,5 cm
= +
= +
≈
9. Ein quaderförmiges Schwimmbecken ist 50 m lang, 25 m breit und 2,60 m
tief.
c) a) Wie viel Kubikmeter Wasser fasst das Becken, wenn es bis zu
20 cm unter dem Beckenrand gefüllt ist?
d) b) Zum Auspumpen des Beckens benutzt man eine Pumpe, die 2 m³
Wasser je Minute fördert. Nach wie viel Stunden ist das Becken
leer?
Lösung a)
V 50 25 2, 4 3000 m³= ⋅ ⋅ =
Lösung b)
Die Pumpe benötigt 1500 Minuten. Dies entspricht 25 Stunden
6. Ein PKW benötigt für 100 km 6,8 Liter Kraftstoff.
c) a) Wie viel Liter Kraftstoff muss man für eine Fahrstrecke von 1
200 km mindestens einplanen?
d) b) Der Tank fasst 43 Liter. Wie viel Kilometer kann man bei
diesem Kraftstoffverbrauch mit einer Tankfüllung maximal fahren?
Lösung a)
Man muss 81,6 Liter einplanen.
Lösung b)
Man schafft ca. 632 km.
Löse die Klammern auf.
a) (x + 3)² = x² + 6x + 9 b) (x – 4)² = x² – 8x + 16
7.
c) (2x + 1)² = 4x² + 4x + 1 d) (x + 3)(x – 3) = x² – 9
8. Trage die folgenden Punkte in ein rechtwinkliges Koordinatensystem ein:
A(0/0), B(4/–2), C(4/0).
c) a) Zeichne das Dreieck ABC.
d) b) Berechne die Länge der Strecke AB.
Lösung a)
A
B
C
-1 1 2 3 4 5
1
-1
-2
Lösung b)
Für die Berechnung wenden wir den „Satz des Pythagoras“ an.
2 2 2
AB AC BC
AB 4² 2²
AB 4,5 cm
= +
= +
≈
9. Ein quaderförmiges Schwimmbecken ist 50 m lang, 25 m breit und 2,60 m
tief.
c) a) Wie viel Kubikmeter Wasser fasst das Becken, wenn es bis zu
20 cm unter dem Beckenrand gefüllt ist?
d) b) Zum Auspumpen des Beckens benutzt man eine Pumpe, die 2 m³
Wasser je Minute fördert. Nach wie viel Stunden ist das Becken
leer?
Lösung a)
V 50 25 2, 4 3000 m³= ⋅ ⋅ =
Lösung b)
Die Pumpe benötigt 1500 Minuten. Dies entspricht 25 Stunden