www.Klassenarbeiten.de Seite 1
Mathematik, 9. Klasse
Stegreifaufgabe Trigonometrie
1. Gegeben sei: sin α = 0,6
Berechne daraus: cos α, cos (90°- α) und tan α
2. Vereinfache so weit wie möglich:
tanα
sinα −tan α ∙sinα =
3. Neigungswinkel einer Diagonalen
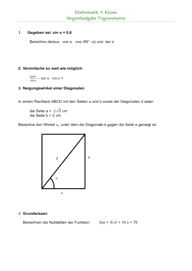
In einem Rechteck ABCD mit den Seiten a und b sowie der Diagonalen d seien
die Seite a = 2 √3 cm
die Seite b = 2 cm
Berechne den Winkel , unter dem die Diagonale d gegen die Seite a geneigt ist.
4. Grundwissen
Berechnen die Nullstellen der Funktion: f(x) = -5 x² + 10 x + 75
a
b d
Mathematik, 9. Klasse
Stegreifaufgabe Trigonometrie
1. Gegeben sei: sin α = 0,6
Berechne daraus: cos α, cos (90°- α) und tan α
2. Vereinfache so weit wie möglich:
tanα
sinα −tan α ∙sinα =
3. Neigungswinkel einer Diagonalen
In einem Rechteck ABCD mit den Seiten a und b sowie der Diagonalen d seien
die Seite a = 2 √3 cm
die Seite b = 2 cm
Berechne den Winkel , unter dem die Diagonale d gegen die Seite a geneigt ist.
4. Grundwissen
Berechnen die Nullstellen der Funktion: f(x) = -5 x² + 10 x + 75
a
b d
www.Klassenarbeiten.de Seite 2
Lösung
Gegeben sei sin α = 0,6
Berechne daraus cos cos (90°- ) und tan
sin = 0,6
sin2(α) + cos2( ) = 1
=> cos2(α) = 1 – sin2( )
cos2(α) = 1 – 0,62
cos2(α)) = 1 – 0,36
cos2(α) = 0,64
cos(α) = 0,8
Vereinfache so weit wie möglich:
tan𝛼
sin𝛼 −tan(𝛼)∙sin(𝛼) =
sinα
cosα ∙ sinα −sin2α
cosα = 1
cosα − sin2α
cosα = 1− sin2α
cosα = cos2α
cosα = cosα
Neigungswinkel einer Diagonalen
In einem Rechteck ABCD mit den Seiten a und b sowie der Diagonalen d seien
die Seite a = 2 √3 cm und die Seite b = 2 cm.
Berechne den Winkel , unter dem die Diagonale d gegen die Seite a geneigt ist.
tanα= 𝑏
𝑎 = 2
2√3 = 1
√3 => 𝛼 =30⁰
4. Grundwissen
Berechnen die Nullstellen der Funktion f (x) = -5 x² + 10 x + 75
Normalform der Gleichung: f (x) = x2 – 2x – 15
x1/2 =− −2
2 ± √(−2
2 )− (−15)
x1/2 =1 ± √ 1+ 15
x1/2 =1 ± √ 16
x1 =1+4 𝐱𝟏 =𝟓
x2 =1−4 𝐱𝟐 =−𝟑
a
b d
cos(90°- ) = sin() = 0,6
tan(α) = sinα
cosα = 0,6
0,8 =0,75
Merke:
Wenn die Gleichung in Normalform
vorliegt, kann man die p-q-Formel
anwenden:
Eine Gleichung der Form
x2 + px + q = 0 hat die Lösungen:
x1/2 =− p
2 ± √(p
2)
2
− q
Lösung
Gegeben sei sin α = 0,6
Berechne daraus cos cos (90°- ) und tan
sin = 0,6
sin2(α) + cos2( ) = 1
=> cos2(α) = 1 – sin2( )
cos2(α) = 1 – 0,62
cos2(α)) = 1 – 0,36
cos2(α) = 0,64
cos(α) = 0,8
Vereinfache so weit wie möglich:
tan𝛼
sin𝛼 −tan(𝛼)∙sin(𝛼) =
sinα
cosα ∙ sinα −sin2α
cosα = 1
cosα − sin2α
cosα = 1− sin2α
cosα = cos2α
cosα = cosα
Neigungswinkel einer Diagonalen
In einem Rechteck ABCD mit den Seiten a und b sowie der Diagonalen d seien
die Seite a = 2 √3 cm und die Seite b = 2 cm.
Berechne den Winkel , unter dem die Diagonale d gegen die Seite a geneigt ist.
tanα= 𝑏
𝑎 = 2
2√3 = 1
√3 => 𝛼 =30⁰
4. Grundwissen
Berechnen die Nullstellen der Funktion f (x) = -5 x² + 10 x + 75
Normalform der Gleichung: f (x) = x2 – 2x – 15
x1/2 =− −2
2 ± √(−2
2 )− (−15)
x1/2 =1 ± √ 1+ 15
x1/2 =1 ± √ 16
x1 =1+4 𝐱𝟏 =𝟓
x2 =1−4 𝐱𝟐 =−𝟑
a
b d
cos(90°- ) = sin() = 0,6
tan(α) = sinα
cosα = 0,6
0,8 =0,75
Merke:
Wenn die Gleichung in Normalform
vorliegt, kann man die p-q-Formel
anwenden:
Eine Gleichung der Form
x2 + px + q = 0 hat die Lösungen:
x1/2 =− p
2 ± √(p
2)
2
− q