www.Klassenarbeiten.de Seite 1
Quadratische Funktionen Arbeitsblatt 1
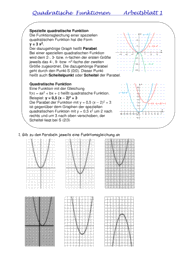
1. Gib zu den Parabeln jeweils eine Funktionsgleichung an
Spezielle quadratische Funktion
Die Funktionsgleichung einer speziellen
quadratischen Funktion hat die Form
y = 3 x2.
Der dazugehörige Graph heißt Parabel.
Bei einer speziellen quadratischen Funktion
wird dem 2-, 3- bzw. n-fachen der ersten Größe
jeweils das 4-, 9- bzw. n2-fache der zweiten
Größe zugeordnet. Die dazugehörige Parabel
geht durch den Punkt S (0|0). Dieser Punkt
heißt auch Scheitelpunkt oder Scheitel der Parabel.
Quadratische Funktion
Eine Funktion mit der Gleichung
f(x) = ax2 + bx + c heißt quadratische Funktion.
Beispiel: y = 0,5 (x – 2)2 + 3
Die Parabel der Funktion mit y = 0,5 (x – 2)2 + 3
ist gegenüber dem Graphen der speziellen
quadratischen Funktion mit y = 0,5 x2 um 2 nach
rechts und um 3 nach oben verschoben; der
Scheitel liegt bei S (2|3)
Quadratische Funktionen Arbeitsblatt 1
1. Gib zu den Parabeln jeweils eine Funktionsgleichung an
Spezielle quadratische Funktion
Die Funktionsgleichung einer speziellen
quadratischen Funktion hat die Form
y = 3 x2.
Der dazugehörige Graph heißt Parabel.
Bei einer speziellen quadratischen Funktion
wird dem 2-, 3- bzw. n-fachen der ersten Größe
jeweils das 4-, 9- bzw. n2-fache der zweiten
Größe zugeordnet. Die dazugehörige Parabel
geht durch den Punkt S (0|0). Dieser Punkt
heißt auch Scheitelpunkt oder Scheitel der Parabel.
Quadratische Funktion
Eine Funktion mit der Gleichung
f(x) = ax2 + bx + c heißt quadratische Funktion.
Beispiel: y = 0,5 (x – 2)2 + 3
Die Parabel der Funktion mit y = 0,5 (x – 2)2 + 3
ist gegenüber dem Graphen der speziellen
quadratischen Funktion mit y = 0,5 x2 um 2 nach
rechts und um 3 nach oben verschoben; der
Scheitel liegt bei S (2|3)
www.Klassenarbeiten.de Seite 2
Quadratische Funktionen Arbeitsblatt 2
1. Erstelle eine Wertetabelle für folgende quadratische Funktionsgleichung
y = x2 + x + 1
x -4 -3 -2 -1 0 1 2 3
y
2. Um eine verschobene Normalparabel zu zeichnen benötigt man den Scheitelpunkt.
Beschreibe, wie man die Parabel auch ohne Schablone zeichnen kann.
_____________________________________________________________
_____________________________________________________________
3. Welche Funktionsgleichung gehört zu welchem Graphen?
y1 = x2 ________
y2 = 2x2 ________
y3 = 0,5x2 ________
y4 = -0,5x2 ________
4. Bestimme den Scheitelpunkt der Parabel, nenne Form und Öffnung.
y = - x2 + 3
y = 2 (x + 1) 2 - 4
y = - 0,5 x2 - 3x - 2,5
y = 0,25 (x - 4) 2
5. Vergleiche Lage und Form des Graphen der vorliegenden Funktion mit der Normal-
parabel. Kreuze an oder trage den entsprechen Wert ein.
Funktionsgleichung verschoben um ..... nach nach unten
geöffnet breiter enger rechts links oben unten
y = 2(x-3)2 + 5 3
y = -(x + 6)2 – 2,5
y = -3x2 + 10
y = 0,2x2 - 5
y = −1
3 (x – 6)2
y = 1
16 (x+1
2)2
Quadratische Funktionen Arbeitsblatt 2
1. Erstelle eine Wertetabelle für folgende quadratische Funktionsgleichung
y = x2 + x + 1
x -4 -3 -2 -1 0 1 2 3
y
2. Um eine verschobene Normalparabel zu zeichnen benötigt man den Scheitelpunkt.
Beschreibe, wie man die Parabel auch ohne Schablone zeichnen kann.
_____________________________________________________________
_____________________________________________________________
3. Welche Funktionsgleichung gehört zu welchem Graphen?
y1 = x2 ________
y2 = 2x2 ________
y3 = 0,5x2 ________
y4 = -0,5x2 ________
4. Bestimme den Scheitelpunkt der Parabel, nenne Form und Öffnung.
y = - x2 + 3
y = 2 (x + 1) 2 - 4
y = - 0,5 x2 - 3x - 2,5
y = 0,25 (x - 4) 2
5. Vergleiche Lage und Form des Graphen der vorliegenden Funktion mit der Normal-
parabel. Kreuze an oder trage den entsprechen Wert ein.
Funktionsgleichung verschoben um ..... nach nach unten
geöffnet breiter enger rechts links oben unten
y = 2(x-3)2 + 5 3
y = -(x + 6)2 – 2,5
y = -3x2 + 10
y = 0,2x2 - 5
y = −1
3 (x – 6)2
y = 1
16 (x+1
2)2
www.Klassenarbeiten.de Seite 3
Quadratische Funktionen Arbeitsblatt 3
1a. Lies die Scheitel ab und gib sie als Koordinatenpaar an (von oben nach unten):
f1: _______ f2: _______
f3: _______ f4: _______
b) Welche Funktionsgleichung gehört zu welchem
Schaubild?
f(x) = x2 – 2 zu _____
f(x) = x2 + 3 zu _____
f(x) = x2 – 5 zu _____
f(x) = x2 + 1 zu _____
c) Ermittle aus den Funktionsgleichungen den
zugehörigen Scheitel.
f(x) = x2 – 1,5 _______
f(x) = x2 + 2,75 _______
f(x) = x2 ______
d) Wie lautet die zugehörige Funktionsgleichung?
S (0|3); S (0|-6);
S (0|-1,25); S (0|1,75)
2. Eine nach unten geöffnete Normalparabel verläuft durch die Punkte A(-1|4) und
B(4|1).
Zeichne die Parabel.
Berechne ihre Funktionsgleichung.
Berechne den Scheitelpunkt.
Stelle durch Rechnung fest, ob der Punkt C(-5|-30) auf der Parabel liegt.
3. Gib eine passende Funktionsgleichung an. Die Normalparabel (y = x2) wurde
a) um 5 Einheiten nach links [y = (x + 5)2] und um 3 Einheiten nach unten verschoben
[y = (x + 5)2 __________]
b) mit dem Faktor 4 gestreckt [y = _____], um 3,5 Einheiten nach oben [ y = __________]
und um 7 Einheiten nach links verschoben [y = _____________]
c) um _____ Einheiten nach _________ verschoben [y = (x – 8)2] und an der x-Achse ge-
spiegelt [y = ___________]
d) so verschoben, dass der Scheitel im Punkt S (__|__) liegt [y = (x + 9)2 – 4] und sie
nach
___________ geöffnet ist [y = -(x + 9)2 – 4]
4. Gib drei verschiedene quadratische Funktionen an, die bei x = 4 die einzige Null-
stelle haben.
Gib drei verschiedene quadratische Funktionen an, die die beiden Nullstellen
x = -1 und x = 1 haben
Quadratische Funktionen Arbeitsblatt 3
1a. Lies die Scheitel ab und gib sie als Koordinatenpaar an (von oben nach unten):
f1: _______ f2: _______
f3: _______ f4: _______
b) Welche Funktionsgleichung gehört zu welchem
Schaubild?
f(x) = x2 – 2 zu _____
f(x) = x2 + 3 zu _____
f(x) = x2 – 5 zu _____
f(x) = x2 + 1 zu _____
c) Ermittle aus den Funktionsgleichungen den
zugehörigen Scheitel.
f(x) = x2 – 1,5 _______
f(x) = x2 + 2,75 _______
f(x) = x2 ______
d) Wie lautet die zugehörige Funktionsgleichung?
S (0|3); S (0|-6);
S (0|-1,25); S (0|1,75)
2. Eine nach unten geöffnete Normalparabel verläuft durch die Punkte A(-1|4) und
B(4|1).
Zeichne die Parabel.
Berechne ihre Funktionsgleichung.
Berechne den Scheitelpunkt.
Stelle durch Rechnung fest, ob der Punkt C(-5|-30) auf der Parabel liegt.
3. Gib eine passende Funktionsgleichung an. Die Normalparabel (y = x2) wurde
a) um 5 Einheiten nach links [y = (x + 5)2] und um 3 Einheiten nach unten verschoben
[y = (x + 5)2 __________]
b) mit dem Faktor 4 gestreckt [y = _____], um 3,5 Einheiten nach oben [ y = __________]
und um 7 Einheiten nach links verschoben [y = _____________]
c) um _____ Einheiten nach _________ verschoben [y = (x – 8)2] und an der x-Achse ge-
spiegelt [y = ___________]
d) so verschoben, dass der Scheitel im Punkt S (__|__) liegt [y = (x + 9)2 – 4] und sie
nach
___________ geöffnet ist [y = -(x + 9)2 – 4]
4. Gib drei verschiedene quadratische Funktionen an, die bei x = 4 die einzige Null-
stelle haben.
Gib drei verschiedene quadratische Funktionen an, die die beiden Nullstellen
x = -1 und x = 1 haben
www.Klassenarbeiten.de Seite 4
Quadratische Funktionen Arbeitsblatt 4
1. Bestimme die Funktionsgleichungen
a) ______________
b) ______________
c) ______________
d) ______________
e) _______________
2. Eigenschaften quadratischer Funktionen
a > 0 a < 0
Die Funktion hat einen kleinsten
Funktionswert (Minimum). Die
Parabel ist nach _____________
geöffnet.
Die Funktion hat einen größten
Funktionswert (Maximum). Die
Parabel ist nach
_______________ geöffnet.
Der Punkt des Graphen, in dem der kleinste bzw. größte
Funktionswert angenommen wird heißt ____________________ S
der Parabel.
Die Parabel ist symmetrisch bezüglich einer Parallelen zur
___________________ durch den Scheitelpunkt S (xS ; yS )
Die Funktion ist monoton fallend
für ________________ für
_____________________
Sie ist monoton wachsend
für ________________ für
_____________________
Für den Wertebereich gilt
WB = { y R ; ___________ } WB = { y R ;
___________ }
Eine quadratische Funktion hat höchstens ________________
Nullstellen.
Quadratische Funktionen Arbeitsblatt 4
1. Bestimme die Funktionsgleichungen
a) ______________
b) ______________
c) ______________
d) ______________
e) _______________
2. Eigenschaften quadratischer Funktionen
a > 0 a < 0
Die Funktion hat einen kleinsten
Funktionswert (Minimum). Die
Parabel ist nach _____________
geöffnet.
Die Funktion hat einen größten
Funktionswert (Maximum). Die
Parabel ist nach
_______________ geöffnet.
Der Punkt des Graphen, in dem der kleinste bzw. größte
Funktionswert angenommen wird heißt ____________________ S
der Parabel.
Die Parabel ist symmetrisch bezüglich einer Parallelen zur
___________________ durch den Scheitelpunkt S (xS ; yS )
Die Funktion ist monoton fallend
für ________________ für
_____________________
Sie ist monoton wachsend
für ________________ für
_____________________
Für den Wertebereich gilt
WB = { y R ; ___________ } WB = { y R ;
___________ }
Eine quadratische Funktion hat höchstens ________________
Nullstellen.
www.Klassenarbeiten.de Seite 5
Quadratische Funktionen Arbeitsblatt 5
1. Stelle für jede der drei Funktionen Wertpaare auf und zeichne den Graph der
Funktion!
a) y = x2 b) y = 3x2 c) y= 1
3x2
2. Gib zwei mögliche Funktionsgleichungen einer quadratischen Funktion an, die
die Bedingung erfüllt.
a) Die Funktion hat keine Nullstelle.
b) Der Graph berührt die x-Achse nur bei x = 2
c) Der Graph ist nach unten geöffnet und die beiden Nullstellen sind
x = -2 und x = 2
d) Die Funktion hat eine Nullstelle bei x = 3 und der Graph geht durch P(2|-2)
3. Stelle für jede der drei Funktionen Wertpaare auf und zeichne den Graph der
Funktion!
a) y = x2 b) y = x2 + 2 c) y = x2 – 2
4. Zeichne die quadratischen Funktionen ohne Wertetabelle in ein Koordinatensystem.
a.) y = (x + 3,5) 2 - 4
b.) y = - x2 - 2
c.) y = x2 - 3x – 4
d.) y = -(x – 4) 2 + 1
e.) Berechne die Nullstellen der Funktion aus d.)
f.) Berechne bei a) den Schnittpunkt mit der y-Achse.
5. Ermittle rechnerisch die Koordinaten des Scheitelpunkts der Parabel, die durch
folgende Gleichung gegeben ist:
y = x2 - 2x + 4 y = −1
2x2 −x−3
2
6. Zeichne den Graph der Funktion mit
y = (x – 3)2 – 1 y = x2 + 2x + 3
7a. Spiegle die Parabel mit der Gleichung y = (x + 2)2 + 1 an der y-Achse.
Die neue Funktionsgleichung lautet: ____________________
b. Spiegle die Parabel mit der Gleichung y = (x + 2)2 + 1 an der x-Achse.
Die neue Funktionsgleichung lautet: ____________________
Quadratische Funktionen Arbeitsblatt 5
1. Stelle für jede der drei Funktionen Wertpaare auf und zeichne den Graph der
Funktion!
a) y = x2 b) y = 3x2 c) y= 1
3x2
2. Gib zwei mögliche Funktionsgleichungen einer quadratischen Funktion an, die
die Bedingung erfüllt.
a) Die Funktion hat keine Nullstelle.
b) Der Graph berührt die x-Achse nur bei x = 2
c) Der Graph ist nach unten geöffnet und die beiden Nullstellen sind
x = -2 und x = 2
d) Die Funktion hat eine Nullstelle bei x = 3 und der Graph geht durch P(2|-2)
3. Stelle für jede der drei Funktionen Wertpaare auf und zeichne den Graph der
Funktion!
a) y = x2 b) y = x2 + 2 c) y = x2 – 2
4. Zeichne die quadratischen Funktionen ohne Wertetabelle in ein Koordinatensystem.
a.) y = (x + 3,5) 2 - 4
b.) y = - x2 - 2
c.) y = x2 - 3x – 4
d.) y = -(x – 4) 2 + 1
e.) Berechne die Nullstellen der Funktion aus d.)
f.) Berechne bei a) den Schnittpunkt mit der y-Achse.
5. Ermittle rechnerisch die Koordinaten des Scheitelpunkts der Parabel, die durch
folgende Gleichung gegeben ist:
y = x2 - 2x + 4 y = −1
2x2 −x−3
2
6. Zeichne den Graph der Funktion mit
y = (x – 3)2 – 1 y = x2 + 2x + 3
7a. Spiegle die Parabel mit der Gleichung y = (x + 2)2 + 1 an der y-Achse.
Die neue Funktionsgleichung lautet: ____________________
b. Spiegle die Parabel mit der Gleichung y = (x + 2)2 + 1 an der x-Achse.
Die neue Funktionsgleichung lautet: ____________________
www.Klassenarbeiten.de Seite 6
Quadratische Funktionen Lösungen 1
1. Gib zu den Parabeln jeweils eine Funktionsgleichung an
y = x2 y = x2 - 2 y = x2 + 1 y = (x – 1)2 y = (x – 1)2 – 3 y = -(x-1) 2 + 4
Quadratische Funktionen Lösungen 2
1. Erstelle eine Wertetabelle für folgende quadratische Funktionsgleichung
y = x2 + x + 1
x -4 -3 -2 -1 0 1 2 3
y 13 7 3 1 1 3 7 13
2. Um eine verschobene Normalparabel zu zeichnen benötigt man den Scheitelpunkt.
Beschreibe, wie man die Parabel auch ohne Schablone zeichnen kann.
Bei einer verschobenen Normalparabel geht man vom Scheitelpunkt um eine Einheit
nach rechts oder links und dann eine Einheit nach oben und erhält zwei weitere Punkte
der Parabel. Anschließend geht man vom Scheitelpunkt zwei Einheiten nach rechts oder
links und dann vier Einheiten nach oben und erhält erneut zwei Punkte der Parabel. In
gleicher Weise erhält man weitere Punkte. Zum Schluss werden die Punkte zu einer
Parabel verbunden.
3. Welche Funktionsgleichung gehört zu welchem Graphen?
y1 = x2 gehört zu Graph 2
y2 = 2x2 gehört zu Graph 3
y3 = 0,5x2 gehört zu Graph 1
y4 = -0,5x2 gehört zu Graph 4
4. Bestimme den Scheitelpunkt der Parabel, nenne Form und Öffnung.
Berechnung des Scheitelpunkts:
y = - x2 + 3 S(0|3), nach unten geöffnete Normalparabel
Quadratische Funktionen Lösungen 1
1. Gib zu den Parabeln jeweils eine Funktionsgleichung an
y = x2 y = x2 - 2 y = x2 + 1 y = (x – 1)2 y = (x – 1)2 – 3 y = -(x-1) 2 + 4
Quadratische Funktionen Lösungen 2
1. Erstelle eine Wertetabelle für folgende quadratische Funktionsgleichung
y = x2 + x + 1
x -4 -3 -2 -1 0 1 2 3
y 13 7 3 1 1 3 7 13
2. Um eine verschobene Normalparabel zu zeichnen benötigt man den Scheitelpunkt.
Beschreibe, wie man die Parabel auch ohne Schablone zeichnen kann.
Bei einer verschobenen Normalparabel geht man vom Scheitelpunkt um eine Einheit
nach rechts oder links und dann eine Einheit nach oben und erhält zwei weitere Punkte
der Parabel. Anschließend geht man vom Scheitelpunkt zwei Einheiten nach rechts oder
links und dann vier Einheiten nach oben und erhält erneut zwei Punkte der Parabel. In
gleicher Weise erhält man weitere Punkte. Zum Schluss werden die Punkte zu einer
Parabel verbunden.
3. Welche Funktionsgleichung gehört zu welchem Graphen?
y1 = x2 gehört zu Graph 2
y2 = 2x2 gehört zu Graph 3
y3 = 0,5x2 gehört zu Graph 1
y4 = -0,5x2 gehört zu Graph 4
4. Bestimme den Scheitelpunkt der Parabel, nenne Form und Öffnung.
Berechnung des Scheitelpunkts:
y = - x2 + 3 S(0|3), nach unten geöffnete Normalparabel
www.Klassenarbeiten.de Seite 7
y = 2 (x + 1) 2 - 4 S(-1|-4), nach oben geöffnete gestreckte Parabel
y = - 0,5 x2 - 3x - 2,5 - 0,5 (x² + 6x + 5) = - 0,5 (x² + 6x + 9 - 4) = - 0,5 (x + 3)2 + 2
→ S(-3|2), nach unten geöffnete gestauchte Parabel
y = 0,25 (x - 4) 2 S(4|0), nach oben geöffnete gestauchte Parabel
5. Vergleiche Lage und Form des Graphen der vorliegenden Funktion mit der Normal-
parabel. Kreuze an oder trage den entsprechen Wert ein.
Funktionsgleichung verschoben um ..... nach nach unten
geöffnet breiter enger rechts links oben unten
y = 2(x – 3)2 + 5 3 5 x
y = -(x + 6)2 – 2,5 6 2,5 x
y = -3x2 + 10 10 x x
y = 0,2x2 - 5 5 x
y = −1
3 (x – 6)2 6 x x
y = 1
16 (x+1
2)2
1
2 x
Quadratische Funktionen Lösungen 3
1a) Lies die Scheitel ab und gib sie als Koordinatenpaar an (von oben nach unten):
f1: S(0|3) f2: S(0|1) f3: S(0|-2) f4: S(0|-5)
b) Welche Funktionsgleichung gehört zu welchem
Schaubild?
f(x) x2 – 2 zu f3 f(x) x2 + 3 zu f1
f(x) x2 – 5 zu f4 f(x) x2 + 1 zu f2
c) Ermittle aus den Funktionsgleichungen den zugehörigen Scheitel.
f(x) x2 – 1,5 S (0|-1,5)
f(x) x2 + 2,75 S (0|2,75)
f(x) x2 S (0|0)
d) Wie lautet die zugehörige Funktionsgleichung?
S (0|3); y = x² + 3 S (0|-6); y = x² - 6
S (0|-1,25); y = x² - 1,25 S (0|1,75) y = x² + 1,75
2. Eine nach unten geöffnete Normalparabel verläuft durch die Punkte A(-1|4) und
B(4|1).
Zeichne die Parabel.
Berechne ihre Funktionsgleichung.
p: y = - x2 + bx + c
A(-1|-4) p → - 4 = - 1 - b + c
B(4|1) p → 1 = - 16 + 4b + c → 5 = - 15 + 5b
→ b = 4 → c = 1
→ p: y = - x2 + 4x + 1
Berechne den Scheitelpunkt.
y = - x2 + 4x + 1
y = - [x2 - 4x - 1]
y = 2 (x + 1) 2 - 4 S(-1|-4), nach oben geöffnete gestreckte Parabel
y = - 0,5 x2 - 3x - 2,5 - 0,5 (x² + 6x + 5) = - 0,5 (x² + 6x + 9 - 4) = - 0,5 (x + 3)2 + 2
→ S(-3|2), nach unten geöffnete gestauchte Parabel
y = 0,25 (x - 4) 2 S(4|0), nach oben geöffnete gestauchte Parabel
5. Vergleiche Lage und Form des Graphen der vorliegenden Funktion mit der Normal-
parabel. Kreuze an oder trage den entsprechen Wert ein.
Funktionsgleichung verschoben um ..... nach nach unten
geöffnet breiter enger rechts links oben unten
y = 2(x – 3)2 + 5 3 5 x
y = -(x + 6)2 – 2,5 6 2,5 x
y = -3x2 + 10 10 x x
y = 0,2x2 - 5 5 x
y = −1
3 (x – 6)2 6 x x
y = 1
16 (x+1
2)2
1
2 x
Quadratische Funktionen Lösungen 3
1a) Lies die Scheitel ab und gib sie als Koordinatenpaar an (von oben nach unten):
f1: S(0|3) f2: S(0|1) f3: S(0|-2) f4: S(0|-5)
b) Welche Funktionsgleichung gehört zu welchem
Schaubild?
f(x) x2 – 2 zu f3 f(x) x2 + 3 zu f1
f(x) x2 – 5 zu f4 f(x) x2 + 1 zu f2
c) Ermittle aus den Funktionsgleichungen den zugehörigen Scheitel.
f(x) x2 – 1,5 S (0|-1,5)
f(x) x2 + 2,75 S (0|2,75)
f(x) x2 S (0|0)
d) Wie lautet die zugehörige Funktionsgleichung?
S (0|3); y = x² + 3 S (0|-6); y = x² - 6
S (0|-1,25); y = x² - 1,25 S (0|1,75) y = x² + 1,75
2. Eine nach unten geöffnete Normalparabel verläuft durch die Punkte A(-1|4) und
B(4|1).
Zeichne die Parabel.
Berechne ihre Funktionsgleichung.
p: y = - x2 + bx + c
A(-1|-4) p → - 4 = - 1 - b + c
B(4|1) p → 1 = - 16 + 4b + c → 5 = - 15 + 5b
→ b = 4 → c = 1
→ p: y = - x2 + 4x + 1
Berechne den Scheitelpunkt.
y = - x2 + 4x + 1
y = - [x2 - 4x - 1]
www.Klassenarbeiten.de Seite 8
y = - [(x - 2) 2 - 4 - 1]
y = - (x - 2) 2 + 5 → S(2|5)
Stelle durch Rechnung fest, ob der Punkt C(-5|-30) auf der Parabel liegt.
C(-5|-30)
y = - (x - 2) 2 + 5
- 30 = - (-5 - 2) 2 + 5
- 30 = - 49 + 5
- 30 = - 44 → C p
3. Gib eine passende Funktionsgleichung an. Die Normalparabel (y = x2) wurde
a) um 5 Einheiten nach links [y = (x + 5)2] und um 3 Einheiten nach unten verschoben
[y = (x + 5)2 - 3]
b) mit dem Faktor 4 gestreckt [y = 4x2], um 3,5 Einheiten nach oben [ y = 4x2 + 3,5]
und um 7 Einheiten nach links verschoben [y = 4(x + 7)2 + 3,5]
c) um 8 Einheiten nach rechts verschoben [y = (x – 8)2] und an der x-Achse ge-
spiegelt [y = -(x – 8)2]
d) so verschoben, dass der Scheitel im Punkt S (-9|-4) liegt [y = (x + 9)2 – 4] und sie nach
unten geöffnet ist [y = -(x + 9)2 – 4]
4. Gib drei verschiedene quadratische Funktionen an, die bei x = 4 die einzige Null-
stelle haben.
y = (4 – 4)2; y = 2(x – 4)2 ; y = -(x – 4) 2
Gib drei verschiedene quadratische Funktionen an, die die beiden Nullstellen
x = -1 und x = 1 haben
y = x2 – 1; y = -x2 + 1; y = 2x2 - 2
Quadratische Funktionen Lösungen 4
1. Bestimme die Funktionsgleichungen
a) y = x2 - 6 b) y = (x – 5 )2 - 6 c) y = (x + 5 )2 - 6
d) y = - (x + 5 )2 + 6 e) y = - (x – 5 )2 + 6
2. Eigenschaften quadratischer Funktionen
a > 0 a < 0
Die Funktion hat einen kleinsten
Funktionswert (Minimum). Die
Parabel ist nach oben geöffnet.
Die Funktion hat einen größten
Funktionswert (Maximum). Die
Parabel ist nach unten geöffnet.
Der Punkt des Graphen, in dem der kleinste bzw. größte
Funktionswert angenommen wird heißt Scheitelpunkt S der Parabel.
Die Parabel ist symmetrisch bezüglich einer Parallelen zur y-Achse
durch den Scheitelpunkt S (xS ; yS )
Die Funktion ist monoton fallend
für x < xS für x > xS
Sie ist monoton wachsend
für x > xS für x < xS
Für den Wertebereich gilt
WB = { y R ; y yS } WB = { y R ; y yS }
Eine quadratische Funktion hat höchstens zwei Nullstellen.
y = - [(x - 2) 2 - 4 - 1]
y = - (x - 2) 2 + 5 → S(2|5)
Stelle durch Rechnung fest, ob der Punkt C(-5|-30) auf der Parabel liegt.
C(-5|-30)
y = - (x - 2) 2 + 5
- 30 = - (-5 - 2) 2 + 5
- 30 = - 49 + 5
- 30 = - 44 → C p
3. Gib eine passende Funktionsgleichung an. Die Normalparabel (y = x2) wurde
a) um 5 Einheiten nach links [y = (x + 5)2] und um 3 Einheiten nach unten verschoben
[y = (x + 5)2 - 3]
b) mit dem Faktor 4 gestreckt [y = 4x2], um 3,5 Einheiten nach oben [ y = 4x2 + 3,5]
und um 7 Einheiten nach links verschoben [y = 4(x + 7)2 + 3,5]
c) um 8 Einheiten nach rechts verschoben [y = (x – 8)2] und an der x-Achse ge-
spiegelt [y = -(x – 8)2]
d) so verschoben, dass der Scheitel im Punkt S (-9|-4) liegt [y = (x + 9)2 – 4] und sie nach
unten geöffnet ist [y = -(x + 9)2 – 4]
4. Gib drei verschiedene quadratische Funktionen an, die bei x = 4 die einzige Null-
stelle haben.
y = (4 – 4)2; y = 2(x – 4)2 ; y = -(x – 4) 2
Gib drei verschiedene quadratische Funktionen an, die die beiden Nullstellen
x = -1 und x = 1 haben
y = x2 – 1; y = -x2 + 1; y = 2x2 - 2
Quadratische Funktionen Lösungen 4
1. Bestimme die Funktionsgleichungen
a) y = x2 - 6 b) y = (x – 5 )2 - 6 c) y = (x + 5 )2 - 6
d) y = - (x + 5 )2 + 6 e) y = - (x – 5 )2 + 6
2. Eigenschaften quadratischer Funktionen
a > 0 a < 0
Die Funktion hat einen kleinsten
Funktionswert (Minimum). Die
Parabel ist nach oben geöffnet.
Die Funktion hat einen größten
Funktionswert (Maximum). Die
Parabel ist nach unten geöffnet.
Der Punkt des Graphen, in dem der kleinste bzw. größte
Funktionswert angenommen wird heißt Scheitelpunkt S der Parabel.
Die Parabel ist symmetrisch bezüglich einer Parallelen zur y-Achse
durch den Scheitelpunkt S (xS ; yS )
Die Funktion ist monoton fallend
für x < xS für x > xS
Sie ist monoton wachsend
für x > xS für x < xS
Für den Wertebereich gilt
WB = { y R ; y yS } WB = { y R ; y yS }
Eine quadratische Funktion hat höchstens zwei Nullstellen.
www.Klassenarbeiten.de Seite 9
Quadratische Funktionen Lösungen 5
1. Stelle für jede der drei Funktionen Wertpaare auf und zeichne den Graph der
Funktion!
a) y = x2 b) y = 3x2 c) y = 1
3x2
a)
b)
c
)
2. Gib zwei mögliche Funktionsgleichungen einer quadratischen Funktion an, die
die Bedingung erfüllt.
a) Die Funktion hat keine Nullstelle.
y = x2 + 1 oder y = x2 + 3 bzw. y = ax2 + c (a und c müssen positive Zahlen sein)
b) Der Graph berührt die x-Achse nur bei x = 2
y = (x – 2)2 oder y = -2(x – 2)2 bzw. y = a(x – 2)2 (mit beliebigem a)
c) Der Graph ist nach unten geöffnet und die beiden Nullstellen sind
x = -2 und x = 2
y = -(x – 2) · (x - 2) = -x2 + 4 oder y = y = -2 (x + 2) · (x – 2) = -2x2 + 8
d) Die Funktion hat eine Nullstelle bei x = 3 und der Graph geht durch P(2|-2)
y = (x – 2)2 – 1 oder y = -(x – 3)2
3. Stelle für jede der drei Funktionen Wertpaare auf und zeichne den Graph der
Funktion!
a) y = x2 b) y = x2 + 2 c) y = x2 – 2
a)
b)
c)
Quadratische Funktionen Lösungen 5
1. Stelle für jede der drei Funktionen Wertpaare auf und zeichne den Graph der
Funktion!
a) y = x2 b) y = 3x2 c) y = 1
3x2
a)
b)
c
)
2. Gib zwei mögliche Funktionsgleichungen einer quadratischen Funktion an, die
die Bedingung erfüllt.
a) Die Funktion hat keine Nullstelle.
y = x2 + 1 oder y = x2 + 3 bzw. y = ax2 + c (a und c müssen positive Zahlen sein)
b) Der Graph berührt die x-Achse nur bei x = 2
y = (x – 2)2 oder y = -2(x – 2)2 bzw. y = a(x – 2)2 (mit beliebigem a)
c) Der Graph ist nach unten geöffnet und die beiden Nullstellen sind
x = -2 und x = 2
y = -(x – 2) · (x - 2) = -x2 + 4 oder y = y = -2 (x + 2) · (x – 2) = -2x2 + 8
d) Die Funktion hat eine Nullstelle bei x = 3 und der Graph geht durch P(2|-2)
y = (x – 2)2 – 1 oder y = -(x – 3)2
3. Stelle für jede der drei Funktionen Wertpaare auf und zeichne den Graph der
Funktion!
a) y = x2 b) y = x2 + 2 c) y = x2 – 2
a)
b)
c)
www.Klassenarbeiten.de Seite 10
4. Zeichne die quadratischen Funktionen ohne Wertetabelle in ein Koordinatensystem.
a) y = (x + 3,5)2 - 4 S (-3,5|-4)
b ) y = - x2 - 2 S (0|-2)
c) y = x2 - 3x – 4 S (1,5|-6,25)
d) y = -(x – 4) 2 + 1 S (4|1)
e) Berechne die Nullstellen der Funktion d)
Nullstellen von d): x1= 5 ; x2=3
Nullstellenberechnung mit der pq-Formel:
(y = x2 + px + q)
y = -(x – 4) 2 + 1
y = -[x2 – 8x + 16] + 1
y = -x2 + 8x – 15
y = (-1) (x2 - 8x + 15) p = -8; q = 15
x1/2 =−p
2 ± √(p
2)2
−q
x1/2 =8
2 ± √(8
2)
2
−15
x1/2 =4 ± √16−15
x1/2 =4 ± √1 x1 = 5; x2 = 3
f) Berechne bei a) den Schnittpunkt mit der y-Achse.
y = (0 + 3,5)2 - 4
y = 12,25 – 4
y = 8,25
5. Ermittle rechnerisch die Koordinaten des Scheitelpunkts der Parabel, die durch
folgende Gleichung gegeben ist:
y = x2 - 2x + 4 y = −1
2x2 −x−3
2
y = x2 - 2x + 1 – 1 + 4 y = −1
2(x2 +2x+3)
y = (x – 1)2 + 3 y = −1
2(x2 +2x+1−1+3)
S = (1|3) y = −1
2 [(x+1)2 +2]
y = −1
2(x+1)2 − 1
S = (-1|-1)
6. Zeichne den Graph der Funktion mit
y = (x – 3)2 – 1 y = x2 + 2x + 3
y = x2 + 2x + 1 – 1 + 3
y = (x + 1) 2 + 2
4. Zeichne die quadratischen Funktionen ohne Wertetabelle in ein Koordinatensystem.
a) y = (x + 3,5)2 - 4 S (-3,5|-4)
b ) y = - x2 - 2 S (0|-2)
c) y = x2 - 3x – 4 S (1,5|-6,25)
d) y = -(x – 4) 2 + 1 S (4|1)
e) Berechne die Nullstellen der Funktion d)
Nullstellen von d): x1= 5 ; x2=3
Nullstellenberechnung mit der pq-Formel:
(y = x2 + px + q)
y = -(x – 4) 2 + 1
y = -[x2 – 8x + 16] + 1
y = -x2 + 8x – 15
y = (-1) (x2 - 8x + 15) p = -8; q = 15
x1/2 =−p
2 ± √(p
2)2
−q
x1/2 =8
2 ± √(8
2)
2
−15
x1/2 =4 ± √16−15
x1/2 =4 ± √1 x1 = 5; x2 = 3
f) Berechne bei a) den Schnittpunkt mit der y-Achse.
y = (0 + 3,5)2 - 4
y = 12,25 – 4
y = 8,25
5. Ermittle rechnerisch die Koordinaten des Scheitelpunkts der Parabel, die durch
folgende Gleichung gegeben ist:
y = x2 - 2x + 4 y = −1
2x2 −x−3
2
y = x2 - 2x + 1 – 1 + 4 y = −1
2(x2 +2x+3)
y = (x – 1)2 + 3 y = −1
2(x2 +2x+1−1+3)
S = (1|3) y = −1
2 [(x+1)2 +2]
y = −1
2(x+1)2 − 1
S = (-1|-1)
6. Zeichne den Graph der Funktion mit
y = (x – 3)2 – 1 y = x2 + 2x + 3
y = x2 + 2x + 1 – 1 + 3
y = (x + 1) 2 + 2
www.Klassenarbeiten.de Seite 11
7a. Spiegle die Parabel mit der Gleichung y = (x + 2)2 + 1 an der y-Achse.
Die neue Funktionsgleichung lautet: y = (x - 2)2 + 1
b. Spiegle die Parabel mit der Gleichung y = (x + 2)2 + 1 an der x-Achse.
Die neue Funktionsgleichung lautet: y = -(x + 2)2 - 1
7a. Spiegle die Parabel mit der Gleichung y = (x + 2)2 + 1 an der y-Achse.
Die neue Funktionsgleichung lautet: y = (x - 2)2 + 1
b. Spiegle die Parabel mit der Gleichung y = (x + 2)2 + 1 an der x-Achse.
Die neue Funktionsgleichung lautet: y = -(x + 2)2 - 1