KA *Quadratische Funktionen*
www.Klassenarbeiten.de Seite 1
Klassenarbeit – Quadratische Funktionen
Schreibe die Rechnungen sorgfältig mit Ansatz, Lösungsweg und Kommentaren auf.
Skizzen sind sorgfältig und mit Lineal zu erstellen, Ergebnisse zu unterstreichen.
Runde die Ergebnisse sinnvoll! Die Arbeitszeit beträgt 45 Minuten.
Aufgabe 1
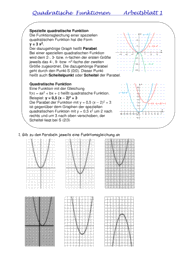
Welche Gleichung gehört zu welchem Graphen? Achtung! Zu einer Gleichung fehlt
der Graph und zu einem Graphen fehlt die Gleichung. Ergänze auch den fehlenden
Graphen und gib die fehlende Gleichung an! (1 Kästchen ≙ 1 Einheit)
a) y = (x – 2)2 b) y = -(x – 3) 2 - 2 c) y = (x + 1) 2 + 1
d) y = -(x + 1) 2 - 2 e) y = (x – 2) 2 + 1 f) y =
1 2 3
6 5 4
www.Klassenarbeiten.de Seite 1
Klassenarbeit – Quadratische Funktionen
Schreibe die Rechnungen sorgfältig mit Ansatz, Lösungsweg und Kommentaren auf.
Skizzen sind sorgfältig und mit Lineal zu erstellen, Ergebnisse zu unterstreichen.
Runde die Ergebnisse sinnvoll! Die Arbeitszeit beträgt 45 Minuten.
Aufgabe 1
Welche Gleichung gehört zu welchem Graphen? Achtung! Zu einer Gleichung fehlt
der Graph und zu einem Graphen fehlt die Gleichung. Ergänze auch den fehlenden
Graphen und gib die fehlende Gleichung an! (1 Kästchen ≙ 1 Einheit)
a) y = (x – 2)2 b) y = -(x – 3) 2 - 2 c) y = (x + 1) 2 + 1
d) y = -(x + 1) 2 - 2 e) y = (x – 2) 2 + 1 f) y =
1 2 3
6 5 4
KA *Quadratische Funktionen*
www.Klassenarbeiten.de Seite 2
Aufgabe 2
Die Funktionsgleichung 𝑓(𝑥)=4𝑥2 + 8𝑥+2 beschreibt eine Parabel.
a) Bestimme den Scheitelpunkt der Parabel!
b) Weise nach, dass der Punkt P (6,2/205,36) auf der Parabel liegt!
c) Gib die Gleichung der Parabel an, die gegen über 𝑓 um eine Einheit nach
unten und um zwei Einheiten nach links verschoben ist!
Aufgabe 3
Ein Ball wird annähernd senkrecht nach oben geworfen. Seine Höhe kann mit der
Funktion ℎ mit ℎ(𝑥)= −5𝑥2 + 17𝑥+1,9, wobei ℎ(𝑡) die Höhe des Balles in Metern
und 𝑡 die Zeit in Sekunden nach dem Abwurf beschreiben.
a) Woher weiß man, dass die Person, die den Ball wirft, ca. 1,90 m groß ist?
b) Ermittle, wie lange der Ball in der Luft ist! (Runde auf Zehntel!)
c) Nach wie vielen Sekunden etwa ist der Ball am höchsten Punkt?
d) Nach wie vielen Sekunden etwa hat der Ball eine Höhe von 4 m erreicht?
Aufgabe 4
Du willst für eine Party an einem See ein rechteckiges
Grundstück abzäunen. Eine Seite wird durch das
gerade verlaufende Ufer gebildet. Für die anderen
Seiten hast du 40 m Absperrband zur Verfügung.
Wie musst du die Seitenlängen wählen, damit der Flächeninhalt maximal wird?
Aufgabe 5
Das Produkt aus dem Quadrat einer Zahl und der um 3 verminderten Zahl ist Null.
Wie lautet die Zahl?
Zusatzaufgabe
Zeige mit Hilfe der p-q-Formel: Sind x1 und x2 die Lösungen einer quadratischen
Gleichung 𝑥2 + 𝑝𝑥+𝑞 =0, so gilt: 𝑝= −(𝑥1 + 𝑥2) und 𝑞 = 𝑥1 ∙ 𝑥2.
www.Klassenarbeiten.de Seite 2
Aufgabe 2
Die Funktionsgleichung 𝑓(𝑥)=4𝑥2 + 8𝑥+2 beschreibt eine Parabel.
a) Bestimme den Scheitelpunkt der Parabel!
b) Weise nach, dass der Punkt P (6,2/205,36) auf der Parabel liegt!
c) Gib die Gleichung der Parabel an, die gegen über 𝑓 um eine Einheit nach
unten und um zwei Einheiten nach links verschoben ist!
Aufgabe 3
Ein Ball wird annähernd senkrecht nach oben geworfen. Seine Höhe kann mit der
Funktion ℎ mit ℎ(𝑥)= −5𝑥2 + 17𝑥+1,9, wobei ℎ(𝑡) die Höhe des Balles in Metern
und 𝑡 die Zeit in Sekunden nach dem Abwurf beschreiben.
a) Woher weiß man, dass die Person, die den Ball wirft, ca. 1,90 m groß ist?
b) Ermittle, wie lange der Ball in der Luft ist! (Runde auf Zehntel!)
c) Nach wie vielen Sekunden etwa ist der Ball am höchsten Punkt?
d) Nach wie vielen Sekunden etwa hat der Ball eine Höhe von 4 m erreicht?
Aufgabe 4
Du willst für eine Party an einem See ein rechteckiges
Grundstück abzäunen. Eine Seite wird durch das
gerade verlaufende Ufer gebildet. Für die anderen
Seiten hast du 40 m Absperrband zur Verfügung.
Wie musst du die Seitenlängen wählen, damit der Flächeninhalt maximal wird?
Aufgabe 5
Das Produkt aus dem Quadrat einer Zahl und der um 3 verminderten Zahl ist Null.
Wie lautet die Zahl?
Zusatzaufgabe
Zeige mit Hilfe der p-q-Formel: Sind x1 und x2 die Lösungen einer quadratischen
Gleichung 𝑥2 + 𝑝𝑥+𝑞 =0, so gilt: 𝑝= −(𝑥1 + 𝑥2) und 𝑞 = 𝑥1 ∙ 𝑥2.
KA *Quadratische Funktionen*
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 3
Aufgabe 1
a) y = (x – 2)2 6 b) y = -(x – 3)2 - 2 2 c) y = (x + 1)2 + 1 4
d) y = -(x + 1)2 - 2 3 e) y = (x – 2)2 + 1 1 f) y = -(x + 2)2 5
Vorgehensweise:
Die Funktionsgleichungen sind in der Scheitelpunktform y=(x+d)2 + e dargestellt. Daher lässt sich
leicht der Scheitelpunkt mit S (-d | e) ablesen.
Steht vor der Klammer ein Minus, so handelt es sich um eine nach unten geöffnete Parabel.
Aufgabe 2
a) Bestimme den Scheitelpunkt der Parabel!
𝑓(𝑥)=4𝑥2 + 8𝑥+2 │4 ausklammern
𝑓(𝑥)= 4(𝑥2 + 2𝑥+ 1
2) │quadratische Ergänzung (𝑝
2)2
addieren und subtrahieren
𝑓(𝑥)= 4(𝑥2 + 2𝑥 + (2
2)2
− (2
2)2
+ 1
2) │binomische Formel anwenden
𝑓(𝑥)= 4((𝑥+1)2 − 1+0,5)) │zusammenfassen u. ausmultiplizieren
𝑓(𝑥)=4(𝑥+1)2 − 4+2
𝑓(𝑥)=4(𝑥+1)2 − 2
Scheitelpunkt ablesen (siehe Erklärung Aufg.1) S (-1 / -2)
b) Weise nach, dass der Punkt P (6,2/205,36) auf der Parabel liegt!
Ein Punkt liegt auf einem Graphen, wenn er die Funktionsgleichung erfüllt. Demzufolge sind die durch
den Punkt gegeben Werte für x und y in die Gleichung einzusetzen. Ergeben sich links und rechts des
Gleichheitszeichens die gleichen Werte, liegt der Punkt auf der Parabel.
Die Funktionsgleichung lautet: 𝑓(𝑥)=4𝑥2 + 8𝑥−2
x = 6,2 und y = 205,36
205,36 = 4 ∙ 6,22 + 8 ∙ 6,2 + 2
205,6 = 4 ∙ 38,44 + 49,6 + 2
205,6 = 153,76 + 49,6 + 2
205,36 = 205,36 wahre Aussage Der Punkt P liegt auf der Parabel.
c) Gib die Gleichung der Parabel an, die gegenüber 𝑓 um eine Einheit nach unten und um zwei Einheiten
nach links verschoben ist!
Ausgehend von der unter a) bestimmten Scheitelpunktform ergibt sich ein neuer Scheitelpunkt
bei (-3 / -4).
Somit ergibt sich: 𝑓𝑛𝑒𝑢(𝑥)=4(𝑥+3)2 − 4=4(𝑥2 +6𝑥+9)− 4=4𝑥²+24𝑥+36−4=4𝑥²+24𝑥+32
Aufgabe 3
Parabel:
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 3
Aufgabe 1
a) y = (x – 2)2 6 b) y = -(x – 3)2 - 2 2 c) y = (x + 1)2 + 1 4
d) y = -(x + 1)2 - 2 3 e) y = (x – 2)2 + 1 1 f) y = -(x + 2)2 5
Vorgehensweise:
Die Funktionsgleichungen sind in der Scheitelpunktform y=(x+d)2 + e dargestellt. Daher lässt sich
leicht der Scheitelpunkt mit S (-d | e) ablesen.
Steht vor der Klammer ein Minus, so handelt es sich um eine nach unten geöffnete Parabel.
Aufgabe 2
a) Bestimme den Scheitelpunkt der Parabel!
𝑓(𝑥)=4𝑥2 + 8𝑥+2 │4 ausklammern
𝑓(𝑥)= 4(𝑥2 + 2𝑥+ 1
2) │quadratische Ergänzung (𝑝
2)2
addieren und subtrahieren
𝑓(𝑥)= 4(𝑥2 + 2𝑥 + (2
2)2
− (2
2)2
+ 1
2) │binomische Formel anwenden
𝑓(𝑥)= 4((𝑥+1)2 − 1+0,5)) │zusammenfassen u. ausmultiplizieren
𝑓(𝑥)=4(𝑥+1)2 − 4+2
𝑓(𝑥)=4(𝑥+1)2 − 2
Scheitelpunkt ablesen (siehe Erklärung Aufg.1) S (-1 / -2)
b) Weise nach, dass der Punkt P (6,2/205,36) auf der Parabel liegt!
Ein Punkt liegt auf einem Graphen, wenn er die Funktionsgleichung erfüllt. Demzufolge sind die durch
den Punkt gegeben Werte für x und y in die Gleichung einzusetzen. Ergeben sich links und rechts des
Gleichheitszeichens die gleichen Werte, liegt der Punkt auf der Parabel.
Die Funktionsgleichung lautet: 𝑓(𝑥)=4𝑥2 + 8𝑥−2
x = 6,2 und y = 205,36
205,36 = 4 ∙ 6,22 + 8 ∙ 6,2 + 2
205,6 = 4 ∙ 38,44 + 49,6 + 2
205,6 = 153,76 + 49,6 + 2
205,36 = 205,36 wahre Aussage Der Punkt P liegt auf der Parabel.
c) Gib die Gleichung der Parabel an, die gegenüber 𝑓 um eine Einheit nach unten und um zwei Einheiten
nach links verschoben ist!
Ausgehend von der unter a) bestimmten Scheitelpunktform ergibt sich ein neuer Scheitelpunkt
bei (-3 / -4).
Somit ergibt sich: 𝑓𝑛𝑒𝑢(𝑥)=4(𝑥+3)2 − 4=4(𝑥2 +6𝑥+9)− 4=4𝑥²+24𝑥+36−4=4𝑥²+24𝑥+32
Aufgabe 3
Parabel:
KA *Quadratische Funktionen*
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 4
Beim Zeichnen der Skizze sollte der Graph am Schnittpunkt mit der y-Achse beginnen und beim
Schnittpunkt mit der x-Achse enden, da der Ball ja nicht in die Erde eindringt.
a) Woher weiß man, dass die Person, die den Ball wirft, ca. 1,90 m groß ist?
Der Schnittpunkt mit der y-Achse (1,9) ist der Abwurfpunkt. Man kann also davon ausgehen, dass der
Ball von einer Höhe von 1,90 m abgeworfen wird. Da man beim Werfen den Arm meist über dem Kopf
hat, ist die werfende Person vermutlich etwas kleiner als 1,90 m.
b) Ermittle, wie lange der Ball in der Luft ist! (Runde auf Zehntel!)
Man benötigt den Zeitpunkt, an dem der Ball auf der Erde auftrifft. Das ist mathematisch der Schnittpunkt
mit der x-Achse, also die Nullstelle. (x / 0) mit x = t.
Lösungen mit Hilfe der p-q-Formel, wobei diese zwei Werte ergeben wird, von denen nur einer der
richtige Wert ist.
h(x) = 0
0= −5𝑥2 + 17𝑥+1,9 │-5 ausklammern
0= −5(𝑥²− 17
5 𝑥− 1,9
5 )
𝑥1/2 = −𝑝
2 ± √(𝑝
2)2
− 𝑞 mit p = −17
5 = -3,4 und q =−1,9
5 = -0,38
Nach Einsetzen in die Formel ergibt sich x1 = 3,5 und x2 = -0,1 (unsinnige Angabe)
Der Ball ist also 3,5 Sekunden in der Luft.
c) Nach wie vielen Sekunden etwa ist der Ball am höchsten Punkt?
Man benötigt den Scheitelpunkt der Parabel, da dies bei der nach unten geöffneten Parabel der höchste
Punkt ist. Der x-Wert des Scheitelpunktes beantwortet die Frage nach dem Zeitpunkt, die y-Koordinate
gibt die Höhe an.
d) Nach wie vielen Sekunden etwa hat der Ball eine Höhe von 4 m erreicht?
Die Höhe ist der bekannte y-Wert, somit muss der dazugehörige x-Wert berechnet werden.
4 = −5𝑥2 + 17𝑥+1,9 │-4
0 = −5𝑥2 + 17𝑥+1,9−4 │-5 ausklammern
0 = −5(𝑥²− 17
5 𝑥+ 2,1
5 )
0 = (𝑥²− 3,4𝑥+ 0,42)
𝑥1/2 = −𝑝
2 ± √(𝑝
2)2
− 𝑞 mit p = -3,4 und q = -0,42
Nach Einsetzen in die Formel ergibt sich x1 = 3,3 und x2 = 0,12.
Der Ball befindet sich einmal nach 0,1 s und einmal nach 3,3 s in 4 m Höhe.
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 4
Beim Zeichnen der Skizze sollte der Graph am Schnittpunkt mit der y-Achse beginnen und beim
Schnittpunkt mit der x-Achse enden, da der Ball ja nicht in die Erde eindringt.
a) Woher weiß man, dass die Person, die den Ball wirft, ca. 1,90 m groß ist?
Der Schnittpunkt mit der y-Achse (1,9) ist der Abwurfpunkt. Man kann also davon ausgehen, dass der
Ball von einer Höhe von 1,90 m abgeworfen wird. Da man beim Werfen den Arm meist über dem Kopf
hat, ist die werfende Person vermutlich etwas kleiner als 1,90 m.
b) Ermittle, wie lange der Ball in der Luft ist! (Runde auf Zehntel!)
Man benötigt den Zeitpunkt, an dem der Ball auf der Erde auftrifft. Das ist mathematisch der Schnittpunkt
mit der x-Achse, also die Nullstelle. (x / 0) mit x = t.
Lösungen mit Hilfe der p-q-Formel, wobei diese zwei Werte ergeben wird, von denen nur einer der
richtige Wert ist.
h(x) = 0
0= −5𝑥2 + 17𝑥+1,9 │-5 ausklammern
0= −5(𝑥²− 17
5 𝑥− 1,9
5 )
𝑥1/2 = −𝑝
2 ± √(𝑝
2)2
− 𝑞 mit p = −17
5 = -3,4 und q =−1,9
5 = -0,38
Nach Einsetzen in die Formel ergibt sich x1 = 3,5 und x2 = -0,1 (unsinnige Angabe)
Der Ball ist also 3,5 Sekunden in der Luft.
c) Nach wie vielen Sekunden etwa ist der Ball am höchsten Punkt?
Man benötigt den Scheitelpunkt der Parabel, da dies bei der nach unten geöffneten Parabel der höchste
Punkt ist. Der x-Wert des Scheitelpunktes beantwortet die Frage nach dem Zeitpunkt, die y-Koordinate
gibt die Höhe an.
d) Nach wie vielen Sekunden etwa hat der Ball eine Höhe von 4 m erreicht?
Die Höhe ist der bekannte y-Wert, somit muss der dazugehörige x-Wert berechnet werden.
4 = −5𝑥2 + 17𝑥+1,9 │-4
0 = −5𝑥2 + 17𝑥+1,9−4 │-5 ausklammern
0 = −5(𝑥²− 17
5 𝑥+ 2,1
5 )
0 = (𝑥²− 3,4𝑥+ 0,42)
𝑥1/2 = −𝑝
2 ± √(𝑝
2)2
− 𝑞 mit p = -3,4 und q = -0,42
Nach Einsetzen in die Formel ergibt sich x1 = 3,3 und x2 = 0,12.
Der Ball befindet sich einmal nach 0,1 s und einmal nach 3,3 s in 4 m Höhe.
KA *Quadratische Funktionen*
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 5
Aufgabe 4
Wie musst du die Seitenlängen wählen, damit der Flächeninhalt maximal wird?
Geg.: u = 40 m
u = 2a + b │nach b umstellen
b = u – 2a = 40 – 2a │b in Flächeninhaltsformel einsetzen
A = ab
A(a) = a(40 – 2a)
A(a) = -2a² + 40a
Quadratische Funktion Scheitelpunkt berechnen, da dort der Flächeninhalt maximal wird. Der x-Wert
des Scheitelpunktes ergibt die Länge der Seite a und der y-Wert ergibt den maximalen Flächeninhalt.
Dazu wird die Gleichung in die Scheitelpunktform gebracht.
A(a) = -2a² + 40a │-2 ausklammern
A(a) = -2(a² - 20a) │quadratische Ergänzung addieren u. subtrahieren
A(a) = -2(a² - 20a + (20
2 )²− (20
2 )²) │ binom. Formel anwenden, zusammenfassen
A(a) = -2((a – 10)² − 100)) │ausmultiplizieren
A(a) = -2(a – 10)² + 200))
S (10 / 200)
Seite a = 10 m
b = 40 – 2 ∙ 10 = 20 m
Wenn die Seite parallel zum Ufer 20 m lang und die andere Seite 10 m lang ist, wird der Flächeninhalt
maximal.
Aufgabe 5
Das Produkt aus dem Quadrat einer Zahl und der um 3 verminderten Zahl ist Null. Wie lautet die Zahl?
x2 (x – 3) = 0 Ein Produkt wird Null, wenn ein Faktor Null ist.
x1 = 0
0 = x – 3 │+3
x2 = 3
Die Zahl kann 0 oder 3 sein.
a
b
See
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 5
Aufgabe 4
Wie musst du die Seitenlängen wählen, damit der Flächeninhalt maximal wird?
Geg.: u = 40 m
u = 2a + b │nach b umstellen
b = u – 2a = 40 – 2a │b in Flächeninhaltsformel einsetzen
A = ab
A(a) = a(40 – 2a)
A(a) = -2a² + 40a
Quadratische Funktion Scheitelpunkt berechnen, da dort der Flächeninhalt maximal wird. Der x-Wert
des Scheitelpunktes ergibt die Länge der Seite a und der y-Wert ergibt den maximalen Flächeninhalt.
Dazu wird die Gleichung in die Scheitelpunktform gebracht.
A(a) = -2a² + 40a │-2 ausklammern
A(a) = -2(a² - 20a) │quadratische Ergänzung addieren u. subtrahieren
A(a) = -2(a² - 20a + (20
2 )²− (20
2 )²) │ binom. Formel anwenden, zusammenfassen
A(a) = -2((a – 10)² − 100)) │ausmultiplizieren
A(a) = -2(a – 10)² + 200))
S (10 / 200)
Seite a = 10 m
b = 40 – 2 ∙ 10 = 20 m
Wenn die Seite parallel zum Ufer 20 m lang und die andere Seite 10 m lang ist, wird der Flächeninhalt
maximal.
Aufgabe 5
Das Produkt aus dem Quadrat einer Zahl und der um 3 verminderten Zahl ist Null. Wie lautet die Zahl?
x2 (x – 3) = 0 Ein Produkt wird Null, wenn ein Faktor Null ist.
x1 = 0
0 = x – 3 │+3
x2 = 3
Die Zahl kann 0 oder 3 sein.
a
b
See
KA *Quadratische Funktionen*
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 6
Zusatzaufgabe
Zeige mit Hilfe der p-q-Formel: Sind x1 und x2 die Lösungen einer quadratischen Gleichung
𝑥2 + 𝑝𝑥+𝑞 =0, so gilt: 𝑝= −(𝑥1 + 𝑥2) und 𝑞 = 𝑥1 ∙ 𝑥2.
x2 + px+q=0
x1/2 = −p
2 ± √(p
2)
2
− q
x1 = −p
2 + √(p
2)2
− q │+(p
2)
x1 +p
2 = √(p
2)2
− q │quadrieren
(x1 +p
2)2
= (p
2)2
− q │binom. Formel anwenden
(x1)²+2⋅ p
2 ⋅ x1 + (p
2)2
= (p
2)2
− q │-(p
2)2
(x1)²+ p ⋅ x1 = − q
Analog dazu ergibt sich für x2 folgende Gleichung (Dass die Wurzel bei x2 subtrahiert wird, spielt keine
Rolle, da wir quadrieren.)
𝑥2 +𝑝
2 = − √(𝑝
2)2
− 𝑞 │quadrieren
(𝑥1 +𝑝
2)2
= (− √(𝑝
2)2
− 𝑞)
2
... (weiter wie oben)
(x2)²+ p ⋅ x2 = − q
Rote Gleichungen gleichsetzen:
(𝑥1)²+ 𝑝 ⋅ 𝑥1 =(𝑥2)²+ 𝑝 ⋅ 𝑥2 │- (𝑥2)²; - px1
(𝑥1)²−(𝑥2)² = 𝑝 ⋅ 𝑥2 − 𝑝 ⋅ 𝑥1 │(-p) ausklammern, 3. binom. Formel anwenden
(𝑥1 − 𝑥2)(𝑥1 + 𝑥2)=−𝑝(−𝑥2 + 𝑥1)
(𝑥1 − 𝑥2)(𝑥1 + 𝑥2)=−𝑝(𝑥1 − 𝑥2) │:(𝑥1 − 𝑥2)
(𝑥1 + 𝑥2)= −𝑝
𝑝 = −(𝑥1 − 𝑥2) w.z.b.w. (qu.e.d)
(𝑥1)²+ 𝑝 ⋅ 𝑥1 = − 𝑞 │nach p umstellen
𝑝= −𝑞−(𝑥1)²
𝑥1
(𝑥2)²+ 𝑝 ⋅ 𝑥2 = − 𝑞 │nach p umstellen
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 6
Zusatzaufgabe
Zeige mit Hilfe der p-q-Formel: Sind x1 und x2 die Lösungen einer quadratischen Gleichung
𝑥2 + 𝑝𝑥+𝑞 =0, so gilt: 𝑝= −(𝑥1 + 𝑥2) und 𝑞 = 𝑥1 ∙ 𝑥2.
x2 + px+q=0
x1/2 = −p
2 ± √(p
2)
2
− q
x1 = −p
2 + √(p
2)2
− q │+(p
2)
x1 +p
2 = √(p
2)2
− q │quadrieren
(x1 +p
2)2
= (p
2)2
− q │binom. Formel anwenden
(x1)²+2⋅ p
2 ⋅ x1 + (p
2)2
= (p
2)2
− q │-(p
2)2
(x1)²+ p ⋅ x1 = − q
Analog dazu ergibt sich für x2 folgende Gleichung (Dass die Wurzel bei x2 subtrahiert wird, spielt keine
Rolle, da wir quadrieren.)
𝑥2 +𝑝
2 = − √(𝑝
2)2
− 𝑞 │quadrieren
(𝑥1 +𝑝
2)2
= (− √(𝑝
2)2
− 𝑞)
2
... (weiter wie oben)
(x2)²+ p ⋅ x2 = − q
Rote Gleichungen gleichsetzen:
(𝑥1)²+ 𝑝 ⋅ 𝑥1 =(𝑥2)²+ 𝑝 ⋅ 𝑥2 │- (𝑥2)²; - px1
(𝑥1)²−(𝑥2)² = 𝑝 ⋅ 𝑥2 − 𝑝 ⋅ 𝑥1 │(-p) ausklammern, 3. binom. Formel anwenden
(𝑥1 − 𝑥2)(𝑥1 + 𝑥2)=−𝑝(−𝑥2 + 𝑥1)
(𝑥1 − 𝑥2)(𝑥1 + 𝑥2)=−𝑝(𝑥1 − 𝑥2) │:(𝑥1 − 𝑥2)
(𝑥1 + 𝑥2)= −𝑝
𝑝 = −(𝑥1 − 𝑥2) w.z.b.w. (qu.e.d)
(𝑥1)²+ 𝑝 ⋅ 𝑥1 = − 𝑞 │nach p umstellen
𝑝= −𝑞−(𝑥1)²
𝑥1
(𝑥2)²+ 𝑝 ⋅ 𝑥2 = − 𝑞 │nach p umstellen
KA *Quadratische Funktionen*
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 7
𝑝= −𝑞−(𝑥2)²
𝑥2
Beide nach p umgestellte Gleichungen gleichsetzen
−𝑞−(𝑥1)²
𝑥1
= −𝑞−(𝑥2)²
𝑥2
│auf den gleichen Nenner bringen
𝑥2(−𝑞−(𝑥1)2)
𝑥1⋅ 𝑥2
= 𝑥1(−𝑞−(𝑥2)2)
𝑥2⋅ 𝑥1
𝑥2(−𝑞−(𝑥1)2)=𝑥1(−𝑞−(𝑥2)2) │ausmultiplizieren
𝑥2 ⋅(−𝑞)−𝑥2(𝑥1)2 =𝑥1(−𝑞)−𝑥1(𝑥2)2
−𝑝𝑥2 − 𝑥2(𝑥1)2 = −𝑝𝑥1 −𝑥1(𝑥2)2 │+𝑝𝑥1; +𝑥2(𝑥1)2
−𝑝𝑥2 +𝑝𝑥1 = −𝑥1(𝑥2)2 +𝑥2(𝑥1)2 │p ausklammern; x1x2 ausklammern
𝑝(−𝑥2 + 𝑥1)= 𝑥1𝑥2(−𝑥2 +𝑥1) │:(− 𝑥2 + 𝑥1)
𝑝= 𝑥1𝑥2
w.z.b.w.
LÖSUNGEN Kl. 9 Gym. Berlin April
www.Klassenarbeiten.de Seite 7
𝑝= −𝑞−(𝑥2)²
𝑥2
Beide nach p umgestellte Gleichungen gleichsetzen
−𝑞−(𝑥1)²
𝑥1
= −𝑞−(𝑥2)²
𝑥2
│auf den gleichen Nenner bringen
𝑥2(−𝑞−(𝑥1)2)
𝑥1⋅ 𝑥2
= 𝑥1(−𝑞−(𝑥2)2)
𝑥2⋅ 𝑥1
𝑥2(−𝑞−(𝑥1)2)=𝑥1(−𝑞−(𝑥2)2) │ausmultiplizieren
𝑥2 ⋅(−𝑞)−𝑥2(𝑥1)2 =𝑥1(−𝑞)−𝑥1(𝑥2)2
−𝑝𝑥2 − 𝑥2(𝑥1)2 = −𝑝𝑥1 −𝑥1(𝑥2)2 │+𝑝𝑥1; +𝑥2(𝑥1)2
−𝑝𝑥2 +𝑝𝑥1 = −𝑥1(𝑥2)2 +𝑥2(𝑥1)2 │p ausklammern; x1x2 ausklammern
𝑝(−𝑥2 + 𝑥1)= 𝑥1𝑥2(−𝑥2 +𝑥1) │:(− 𝑥2 + 𝑥1)
𝑝= 𝑥1𝑥2
w.z.b.w.