www.Klassenarbeiten.de Seite 1
Flächeninhalt und Umfang 8. Klasse 1 Rechne alle Aufgaben auf einem Extrablatt und trage nur die Ergebnisse ein!
1. Ein Rechteck mit dem Flächeninhalt 28m² ist 7m lang. Wie breit ist es?
Antwort: __________________________________________________________
2. Der Umfang eines rechteckigen Grundstückes beträgt 240 m. Die andere Seite
ist dreimal so lang wie die andere Seite. Wie lang sind die Seiten?
Antwort: __________________________________________________________
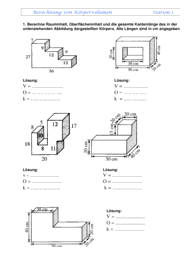
3. Berechne den Flächeninhalt und den Umfang der Figuren
U = ____________ U = ___________ U = __________ U = ___________
A = ____________ A = ___________ A = __________ A = ___________
4. Fülle die Tabelle für die Parallelogramme aus
a b ha hb u A
25 cm 15 cm 90 cm²
12 m 8 m 120 m²
18 dm 7 dm 80 dm
5. Das Treppenhaus zum Keller soll neu gestrichen werden.
Damit die Farbe gut deckt, muss die Wandfläche zweimal gestrichen werden.
a) Berechne die zu streichende Fläche.
b) Für die Farbe kommen zwei Angebot für die 5-l-Eimer
infrage. Erkläre, warum Hr. Keller sich gegen das preis-
wertere Angebot entscheidet.
6. Der Flächeninhalt eines Parallelogramms ergibt sich als Produkt einer Seitenlänge
und der Länge der zugehörigen ____________.
Bei der Raute sind alle Seiten ________ lang.
Flächeninhalt und Umfang 8. Klasse 1 Rechne alle Aufgaben auf einem Extrablatt und trage nur die Ergebnisse ein!
1. Ein Rechteck mit dem Flächeninhalt 28m² ist 7m lang. Wie breit ist es?
Antwort: __________________________________________________________
2. Der Umfang eines rechteckigen Grundstückes beträgt 240 m. Die andere Seite
ist dreimal so lang wie die andere Seite. Wie lang sind die Seiten?
Antwort: __________________________________________________________
3. Berechne den Flächeninhalt und den Umfang der Figuren
U = ____________ U = ___________ U = __________ U = ___________
A = ____________ A = ___________ A = __________ A = ___________
4. Fülle die Tabelle für die Parallelogramme aus
a b ha hb u A
25 cm 15 cm 90 cm²
12 m 8 m 120 m²
18 dm 7 dm 80 dm
5. Das Treppenhaus zum Keller soll neu gestrichen werden.
Damit die Farbe gut deckt, muss die Wandfläche zweimal gestrichen werden.
a) Berechne die zu streichende Fläche.
b) Für die Farbe kommen zwei Angebot für die 5-l-Eimer
infrage. Erkläre, warum Hr. Keller sich gegen das preis-
wertere Angebot entscheidet.
6. Der Flächeninhalt eines Parallelogramms ergibt sich als Produkt einer Seitenlänge
und der Länge der zugehörigen ____________.
Bei der Raute sind alle Seiten ________ lang.
www.Klassenarbeiten.de Seite 2
Flächeninhalt und Umfang 8. Klasse 2
1. Tobi möchte sein Zimmer streichen. Die Grundfarbe der Wand soll Orange sein,
außerdem soll die Wand einen 30 cm breiten gelben Streifen (direkt über dem
Boden) haben.
a) Wie viel m² muss Tobi in orange
streichen und für wie viel m² muss er
gelbe Farbe kaufen?
Antwort: __________________
b) Zusätzlich sollen in Tobis und Lenas
Zimmer Laminatboden und Fußleisten
verlegt werden. Wie viel m2 Laminat und
Fußleisten muss die Familie kaufen?
Antwort: _____________________________
2. Zwei Straßen sind 5,50 m und 7,50 m breit. Sie kreuzen sich unter einem Winkel
von 60°. Wie groß ist der Flächeninhalt der Kreuzung? Fertige eine Zeichnung an.
Antwort: __________________________________________________________
3. Berechne die Fläche des Dreiecks für
a = 2 cm; ha = 3 cm a = 8 cm; ha = 5 cm a = 5,5 cm; ha = 3 cm
4. Berechne den Umfang eines Dreiecks mit den angegebenen Seitenlängen.
a = 6 cm; b = 3 cm; c = 10cm a = 8,2 mm; b = 4,5 mm; c = 13,7 mm
a = 6,8 km; b= 3100 m; c = 211 m
5. Der Flächeninhalt eines Trapezes wird aus den ________ der beiden parallelen
Seiten und der Höhe berechnet.
6. Berechne die fehlenden Größen eines Trapezes.
a) b) c) d) e) f)
a 7,6 cm 8 cm 12 dm 14,4 km 4,5 cm
c 3,4 cm 1,8 m 8 dm 7,2 km
h 4 cm 4,2 cm 90 cm 4,8 dm 2,5 cm
A 27,3 cm² 2,25 m² 27 km² 8,5 cm²
7. Zeichne die Punkte in ein Koordinatensystem und verbinde sie. Berechne den
Flächeninhalt der Vierecke ABCD.
a) A(1/0); B(4,5/0); C(4,5/3); D(1/3,5) b) A(4/0); B(6/3); C(3/7); D(1/3)
c) A(-2,5/-2); B(-1/0); C(-2,5/2); D(-4/0) d) A(1/1); B(4/6); C(8/1); D(5/3)
Flächeninhalt und Umfang 8. Klasse 2
1. Tobi möchte sein Zimmer streichen. Die Grundfarbe der Wand soll Orange sein,
außerdem soll die Wand einen 30 cm breiten gelben Streifen (direkt über dem
Boden) haben.
a) Wie viel m² muss Tobi in orange
streichen und für wie viel m² muss er
gelbe Farbe kaufen?
Antwort: __________________
b) Zusätzlich sollen in Tobis und Lenas
Zimmer Laminatboden und Fußleisten
verlegt werden. Wie viel m2 Laminat und
Fußleisten muss die Familie kaufen?
Antwort: _____________________________
2. Zwei Straßen sind 5,50 m und 7,50 m breit. Sie kreuzen sich unter einem Winkel
von 60°. Wie groß ist der Flächeninhalt der Kreuzung? Fertige eine Zeichnung an.
Antwort: __________________________________________________________
3. Berechne die Fläche des Dreiecks für
a = 2 cm; ha = 3 cm a = 8 cm; ha = 5 cm a = 5,5 cm; ha = 3 cm
4. Berechne den Umfang eines Dreiecks mit den angegebenen Seitenlängen.
a = 6 cm; b = 3 cm; c = 10cm a = 8,2 mm; b = 4,5 mm; c = 13,7 mm
a = 6,8 km; b= 3100 m; c = 211 m
5. Der Flächeninhalt eines Trapezes wird aus den ________ der beiden parallelen
Seiten und der Höhe berechnet.
6. Berechne die fehlenden Größen eines Trapezes.
a) b) c) d) e) f)
a 7,6 cm 8 cm 12 dm 14,4 km 4,5 cm
c 3,4 cm 1,8 m 8 dm 7,2 km
h 4 cm 4,2 cm 90 cm 4,8 dm 2,5 cm
A 27,3 cm² 2,25 m² 27 km² 8,5 cm²
7. Zeichne die Punkte in ein Koordinatensystem und verbinde sie. Berechne den
Flächeninhalt der Vierecke ABCD.
a) A(1/0); B(4,5/0); C(4,5/3); D(1/3,5) b) A(4/0); B(6/3); C(3/7); D(1/3)
c) A(-2,5/-2); B(-1/0); C(-2,5/2); D(-4/0) d) A(1/1); B(4/6); C(8/1); D(5/3)
www.Klassenarbeiten.de Seite 3
Flächeninhalt und Umfang 8. Klasse 3
1. Zeichne das Parallelogramm ABCD mit A(4|1), B(7|1), C(3|5) und D(0|5) in ein
Koordinatensystem.
a) Bestimme den Flächeninhalt in cm²
b) Berechne den Umfang
c) Berechne die Höhe hb (runde)
d) Trage den Punkt E(1,5|2,5) ein. Verbinde ihn mit C und A. Wo muss F liegen,
damit daraus die Raute EAFC entsteht? F (__|__)
2. Berechne den Flächeninhalt der folgenden Dreiecke.
a = 7,4 cm; ha = 3,6 cm c = 70,4 m; hc = 44,8 m
b = 12,3 dm; hb = 88 cm a = 6,4 cm; ha = 3,6 cm
3. Zeichne die folgenden Trapeze und berechne ihren Flächeninhalt.
a) a = 7,5 cm; b = 4,5 cm; c = 3,8 cm; ß = 50°
b) a = 9,5 cm; b = 4 cm; e = 8,6 cm; = 110°
c) a = 5,5 cm; c = 4,7 cm; e = 5,6 cm; ß = 54°
4. Berechne die gesuchte Länge.
Rechteck A = 240 cm²; b = 30 cm; a = ?
Dreieck A = 48 cm²; g = 10 cm; h = ?
Parallelogramm U = 124 m; a = 42 m; b = ?
Parallelogramm A = 96 cm²; h = 6 cm; g = ?
Trapez A = 630 cm²; h = 30 cm; a = 7 cm; c = ?
Trapez A = 360 cm²; a = 6 cm; c = 3 cm; h = ?
5. Bestimme den Flächeninhalt der Figuren durch geschickte Zerlegung. Zeichne
diese ein und notiere die Flächeninhalte der Teilflächen in der Zeichnung.
6. Berechne die folgenden Giebelflächen.
Flächeninhalt und Umfang 8. Klasse 3
1. Zeichne das Parallelogramm ABCD mit A(4|1), B(7|1), C(3|5) und D(0|5) in ein
Koordinatensystem.
a) Bestimme den Flächeninhalt in cm²
b) Berechne den Umfang
c) Berechne die Höhe hb (runde)
d) Trage den Punkt E(1,5|2,5) ein. Verbinde ihn mit C und A. Wo muss F liegen,
damit daraus die Raute EAFC entsteht? F (__|__)
2. Berechne den Flächeninhalt der folgenden Dreiecke.
a = 7,4 cm; ha = 3,6 cm c = 70,4 m; hc = 44,8 m
b = 12,3 dm; hb = 88 cm a = 6,4 cm; ha = 3,6 cm
3. Zeichne die folgenden Trapeze und berechne ihren Flächeninhalt.
a) a = 7,5 cm; b = 4,5 cm; c = 3,8 cm; ß = 50°
b) a = 9,5 cm; b = 4 cm; e = 8,6 cm; = 110°
c) a = 5,5 cm; c = 4,7 cm; e = 5,6 cm; ß = 54°
4. Berechne die gesuchte Länge.
Rechteck A = 240 cm²; b = 30 cm; a = ?
Dreieck A = 48 cm²; g = 10 cm; h = ?
Parallelogramm U = 124 m; a = 42 m; b = ?
Parallelogramm A = 96 cm²; h = 6 cm; g = ?
Trapez A = 630 cm²; h = 30 cm; a = 7 cm; c = ?
Trapez A = 360 cm²; a = 6 cm; c = 3 cm; h = ?
5. Bestimme den Flächeninhalt der Figuren durch geschickte Zerlegung. Zeichne
diese ein und notiere die Flächeninhalte der Teilflächen in der Zeichnung.
6. Berechne die folgenden Giebelflächen.
www.Klassenarbeiten.de Seite 4
Flächeninhalt und Umfang 8. Klasse 4
1. Berechne aus dem Flächeninhalt eines Dreiecks und der Länge einer Seite die
zugehörige Höhe.
A = 18,9 cm²; c = 7 cm A = 13,5 cm²; a = 4,5 cm
A = 32,2 cm²; b = 14 cm A = 49,5 cm; c = 15 cm
2. Berechne die fehlenden Größen eines Drachen.
a) b) c) d) e) f)
e 5,2 cm 3,6 cm 9,3 cm 2,4 dm
f 8,4 cm 4,2 cm 5,8 cm 18,4 cm
A 18 cm² 21,42 cm² 7,68 dm² 248,4 cm²
3. Bestimme den Flächeninhalt der Figuren durch geschickte Ergänzung. Notiere
die Flächeninhalte der Teilflächen in der Zeichnung.
4. Berechne den Flächeninhalt des Fünfecks ABCDE
a) A(3/1); B(8/1); C(6/5); D(7/8); E(1/5)
b) A(3/0); B(8/2); C(7/6); D(3/8); E(1/4)
5. Wie groß ist der Flächeninhalt eines Quadrates mit der Diagonalen e = 6 cm?
6. Konstruiere einen Drachen aus den gegebenen Größen. Entnimm die fehlenden
Maße der Zeichnung und berechne den Flächeninhalt.
a) a = 6 cm; d = 4 cm; f = 7,6 cm
b) b = 5 cm; c = 3,6 cm; = 1300
7. Berechne die fehlenden Größen eines Parallelogramms.
a) b) c) d) e) f)
g 4,4 cm 5,4 cm 40 cm 5,5 m
h 2,2 cm 35 dm 60 cm 3,2 km
A 17,6 cm² 8,4 m² 96,25 m² 19,2 km²
Flächeninhalt und Umfang 8. Klasse 4
1. Berechne aus dem Flächeninhalt eines Dreiecks und der Länge einer Seite die
zugehörige Höhe.
A = 18,9 cm²; c = 7 cm A = 13,5 cm²; a = 4,5 cm
A = 32,2 cm²; b = 14 cm A = 49,5 cm; c = 15 cm
2. Berechne die fehlenden Größen eines Drachen.
a) b) c) d) e) f)
e 5,2 cm 3,6 cm 9,3 cm 2,4 dm
f 8,4 cm 4,2 cm 5,8 cm 18,4 cm
A 18 cm² 21,42 cm² 7,68 dm² 248,4 cm²
3. Bestimme den Flächeninhalt der Figuren durch geschickte Ergänzung. Notiere
die Flächeninhalte der Teilflächen in der Zeichnung.
4. Berechne den Flächeninhalt des Fünfecks ABCDE
a) A(3/1); B(8/1); C(6/5); D(7/8); E(1/5)
b) A(3/0); B(8/2); C(7/6); D(3/8); E(1/4)
5. Wie groß ist der Flächeninhalt eines Quadrates mit der Diagonalen e = 6 cm?
6. Konstruiere einen Drachen aus den gegebenen Größen. Entnimm die fehlenden
Maße der Zeichnung und berechne den Flächeninhalt.
a) a = 6 cm; d = 4 cm; f = 7,6 cm
b) b = 5 cm; c = 3,6 cm; = 1300
7. Berechne die fehlenden Größen eines Parallelogramms.
a) b) c) d) e) f)
g 4,4 cm 5,4 cm 40 cm 5,5 m
h 2,2 cm 35 dm 60 cm 3,2 km
A 17,6 cm² 8,4 m² 96,25 m² 19,2 km²
www.Klassenarbeiten.de Seite 5
Flächeninhalt und Umfang 8. Klasse 5
1. Konstruiere ein Dreieck aus a = 5,6 cm; b = 4,8 cm und c = 6,2 cm. Zeichne in das
Dreieck die drei Höhen ein und berechne dreimal aus einer Seite und der
dazugehörigen Höhe den Flächeninhalt.
2. Berechne die fehlende Größe des Trapezes
A = 216 cm²; h = 8 cm; c = 24 cm; a = ?
A = 810 m²; h = 18 m; a = 53 m; c = ?
3. Ein Haus soll verklinkert werden. Wie groß ist die Fläche, wenn für Fenster und
Türen 22% der Gesamtfläche abgerechnet werden?
4. Berechne den Flächeninhalt der dick umrandeten Fläche
5. In einem Parallelogramm ist a = 7,6 cm, b = 3 cm, ha = 2,8 cm. Bestimme hb durch
Zeichnung und durch Rechnung.
10 cm
8 cm
Flächeninhalt und Umfang 8. Klasse 5
1. Konstruiere ein Dreieck aus a = 5,6 cm; b = 4,8 cm und c = 6,2 cm. Zeichne in das
Dreieck die drei Höhen ein und berechne dreimal aus einer Seite und der
dazugehörigen Höhe den Flächeninhalt.
2. Berechne die fehlende Größe des Trapezes
A = 216 cm²; h = 8 cm; c = 24 cm; a = ?
A = 810 m²; h = 18 m; a = 53 m; c = ?
3. Ein Haus soll verklinkert werden. Wie groß ist die Fläche, wenn für Fenster und
Türen 22% der Gesamtfläche abgerechnet werden?
4. Berechne den Flächeninhalt der dick umrandeten Fläche
5. In einem Parallelogramm ist a = 7,6 cm, b = 3 cm, ha = 2,8 cm. Bestimme hb durch
Zeichnung und durch Rechnung.
10 cm
8 cm
www.Klassenarbeiten.de Seite 6
Flächeninhalt und Umfang Lösung 8. Klasse 1
1. Ein Rechteck mit dem Flächeninhalt 28m² ist 7m lang. Wie breit ist es?
Gegeben: ARechteck = 28m² : b = 7m
Gesucht: b
Lösung: AR = l • b => b = AR : l
b = 28m² : 7m
b = 4 cm
Antwort: Das Rechteck ist 4 cm breit.
2. Der Umfang eines rechteckigen Grundstückes beträgt 240 m. Die eine Seite
ist dreimal so lang wie die andere Seite. Wie lang sind die Seiten?
Gegeben: UR = 2 • l + 2 • b (eine Seite: x, andere Seite: 3x)
240 = 2 • 3x + 2 • x
240 = 8x | :8
30 = x
b = 30
l = 90
Antwort: Die eine Seite des Rechtecks ist 30 m lang, die andere 90 m.
3. Berechne den Flächeninhalt und den Umfang der Figuren
a) U = 2 · 6 m + 4 m + 2 · 1 m + 2 m + 2 · 3 m = 26 m
A = 6 m · 3 m + 3 m · 2 m + 4m · 1 m = 28 m²
b) U = 5 m + 2 · 4 m + 1m + 4 · 2 m = 22 m
A = 5 m · 4 m – 2 m · 2 m = 16 m² oder 5 m ∙ 4 m – 2 m ∙ 2 m = 16 m2
c) U = 4 · 1,20 m + 3 · 0,8 m + 1,60 m = 4,8 m + 2,4 m + 1,6 m = 8,8 m
A = 2,40 m · 2 m – 1,2 m · 0,8 m – 0,8 m · 0,8 m = 4,8 m2 – 0,96 m2 - 0,64 m2 = 3,2 m²
d) U = 22 · 0,5 m = 11 m
A = 16 · 0,5² = 4 m²
4. Fülle die Tabelle für die Parallelogramme aus
a b ha hb u A
25 cm 15 cm 3,6 cm 6 cm 80 cm 90 cm²
10 m 15 m 12 m 8 m 50 m 120 m²
18 dm 22 dm 7 dm 5,72̅̅̅̅ dm 80 dm 126 dm²
Fläche des Parallelogramms: A = a ∙ ha oder A = b ∙ hb
Umfang des Parallelogramms : U = 2 ∙ a + 2∙ b = 2∙(a +b)
5. Das Treppenhaus zum Keller soll neu gestrichen werden.
Damit die Farbe gut deckt, muss die Wandfläche zweimal
gestrichen werden.
Flächeninhalt und Umfang Lösung 8. Klasse 1
1. Ein Rechteck mit dem Flächeninhalt 28m² ist 7m lang. Wie breit ist es?
Gegeben: ARechteck = 28m² : b = 7m
Gesucht: b
Lösung: AR = l • b => b = AR : l
b = 28m² : 7m
b = 4 cm
Antwort: Das Rechteck ist 4 cm breit.
2. Der Umfang eines rechteckigen Grundstückes beträgt 240 m. Die eine Seite
ist dreimal so lang wie die andere Seite. Wie lang sind die Seiten?
Gegeben: UR = 2 • l + 2 • b (eine Seite: x, andere Seite: 3x)
240 = 2 • 3x + 2 • x
240 = 8x | :8
30 = x
b = 30
l = 90
Antwort: Die eine Seite des Rechtecks ist 30 m lang, die andere 90 m.
3. Berechne den Flächeninhalt und den Umfang der Figuren
a) U = 2 · 6 m + 4 m + 2 · 1 m + 2 m + 2 · 3 m = 26 m
A = 6 m · 3 m + 3 m · 2 m + 4m · 1 m = 28 m²
b) U = 5 m + 2 · 4 m + 1m + 4 · 2 m = 22 m
A = 5 m · 4 m – 2 m · 2 m = 16 m² oder 5 m ∙ 4 m – 2 m ∙ 2 m = 16 m2
c) U = 4 · 1,20 m + 3 · 0,8 m + 1,60 m = 4,8 m + 2,4 m + 1,6 m = 8,8 m
A = 2,40 m · 2 m – 1,2 m · 0,8 m – 0,8 m · 0,8 m = 4,8 m2 – 0,96 m2 - 0,64 m2 = 3,2 m²
d) U = 22 · 0,5 m = 11 m
A = 16 · 0,5² = 4 m²
4. Fülle die Tabelle für die Parallelogramme aus
a b ha hb u A
25 cm 15 cm 3,6 cm 6 cm 80 cm 90 cm²
10 m 15 m 12 m 8 m 50 m 120 m²
18 dm 22 dm 7 dm 5,72̅̅̅̅ dm 80 dm 126 dm²
Fläche des Parallelogramms: A = a ∙ ha oder A = b ∙ hb
Umfang des Parallelogramms : U = 2 ∙ a + 2∙ b = 2∙(a +b)
5. Das Treppenhaus zum Keller soll neu gestrichen werden.
Damit die Farbe gut deckt, muss die Wandfläche zweimal
gestrichen werden.
www.Klassenarbeiten.de Seite 7
a) Berechne die zu streichende Fläche.
A = 2 · (3 m · 1,4 m + 3m · 2,6 m + 3 m · 1,2 m) = 31,20 m²
b) Für die Farbe kommen zwei Angebot für die 5-l-Eimer infrage. Erkläre, warum Hr.
Keller sich gegen das preiswertere Angebot entscheidet.
preiswertes Angebot:
170 ml reichen für 1 m² - 5 l reichen für 5000
170 m2 = 29,4 m²
Bei diesem Angebot bräuchte er 2 Eimer Farbe : 2 ∙ 14,99 € = 29,98 €
150 ml reichen für 1 m² - 5 l reichen für 5000
150 m2 = 33,3 m²
Bei diesem Angebot bräuchte er nur einen Eimer Farbe zu 16,99 €
Er entscheidet sich für das teurere Angebot, da er von diesem nur einen Eimer benötigt. Bei
der billigeren Farbe würde er zwei Eimer brauchen, welche dann aber 29,98 € kosten
würden.
6. Der Flächeninhalt eines Parallelogramms ergibt sich als Produkt einer Seitenlänge
und der Länge der zugehörigen Höhe.
Bei der Raute sind alle Seiten gleich lang.
Flächeninhalt und Umfang Lösung 8. Klasse 2
1. Tobi möchte sein Zimmer streichen. Die Grundfarbe der Wand soll Orange sein,
außerdem soll die Wand einen 30 cm breiten gelben Streifen (direkt über dem
Boden) haben.
a) Wände ohne Fenster und Türen:
A = (2 · 4 m ∙ 2,5 m + 2 · 4,50 m ∙ 2,5 m) =
20 m2 + 22,5 m2 = 42,5 m2
Fenster: 1,5 m ∙ 1 m = 1,5 m2
Türen: 2 ∙( 2 m ∙ 1 m ) = 4 m2
Gesamtfläche der Wände:
42,5 m2 – 1,5 m2 – 4 m2 = 37 m2
Gelber Streifen: (2 ∙ 4 m + 2 ∙ 4,5 m – 2 ∙ 1 m ) ∙ 0,3 m
4,5 m2
Orange Fläche: 37 m2 – 4,5 m2 = 32,5 m2
Antwort: Tobi muss für 32,5 m2 orange Farbe kaufen und für 4,5 m2 gelbe Farbe.
b) Zusätzlich sollen in Tobis und Lenas Zimmer Laminatboden und Fußleisten
verlegt werden. Wie viel m² Laminat und Fußleisten muss die Familie kaufen?
Laminat:
In Tobis Zimmer: 4,50 m · 4 m = 18 m2 In Lenas Zimmer: 3,50 m · 5 m = 17,5 m2
Für beide Zimmer: 18 m2 + 17,5 m2= 35,5 m2
Fußleisten:
(4 m + 4,5 m + 3 m + 3,5 m) + (4 m + 3,5 m + 5 m + 2,5 m) = 15 m + 15 m = 30 m
Antwort: Für beide Zimmer müssen sie 35,5 m2 Laminat kaufen und 30 m Fußleisten.
a) Berechne die zu streichende Fläche.
A = 2 · (3 m · 1,4 m + 3m · 2,6 m + 3 m · 1,2 m) = 31,20 m²
b) Für die Farbe kommen zwei Angebot für die 5-l-Eimer infrage. Erkläre, warum Hr.
Keller sich gegen das preiswertere Angebot entscheidet.
preiswertes Angebot:
170 ml reichen für 1 m² - 5 l reichen für 5000
170 m2 = 29,4 m²
Bei diesem Angebot bräuchte er 2 Eimer Farbe : 2 ∙ 14,99 € = 29,98 €
150 ml reichen für 1 m² - 5 l reichen für 5000
150 m2 = 33,3 m²
Bei diesem Angebot bräuchte er nur einen Eimer Farbe zu 16,99 €
Er entscheidet sich für das teurere Angebot, da er von diesem nur einen Eimer benötigt. Bei
der billigeren Farbe würde er zwei Eimer brauchen, welche dann aber 29,98 € kosten
würden.
6. Der Flächeninhalt eines Parallelogramms ergibt sich als Produkt einer Seitenlänge
und der Länge der zugehörigen Höhe.
Bei der Raute sind alle Seiten gleich lang.
Flächeninhalt und Umfang Lösung 8. Klasse 2
1. Tobi möchte sein Zimmer streichen. Die Grundfarbe der Wand soll Orange sein,
außerdem soll die Wand einen 30 cm breiten gelben Streifen (direkt über dem
Boden) haben.
a) Wände ohne Fenster und Türen:
A = (2 · 4 m ∙ 2,5 m + 2 · 4,50 m ∙ 2,5 m) =
20 m2 + 22,5 m2 = 42,5 m2
Fenster: 1,5 m ∙ 1 m = 1,5 m2
Türen: 2 ∙( 2 m ∙ 1 m ) = 4 m2
Gesamtfläche der Wände:
42,5 m2 – 1,5 m2 – 4 m2 = 37 m2
Gelber Streifen: (2 ∙ 4 m + 2 ∙ 4,5 m – 2 ∙ 1 m ) ∙ 0,3 m
4,5 m2
Orange Fläche: 37 m2 – 4,5 m2 = 32,5 m2
Antwort: Tobi muss für 32,5 m2 orange Farbe kaufen und für 4,5 m2 gelbe Farbe.
b) Zusätzlich sollen in Tobis und Lenas Zimmer Laminatboden und Fußleisten
verlegt werden. Wie viel m² Laminat und Fußleisten muss die Familie kaufen?
Laminat:
In Tobis Zimmer: 4,50 m · 4 m = 18 m2 In Lenas Zimmer: 3,50 m · 5 m = 17,5 m2
Für beide Zimmer: 18 m2 + 17,5 m2= 35,5 m2
Fußleisten:
(4 m + 4,5 m + 3 m + 3,5 m) + (4 m + 3,5 m + 5 m + 2,5 m) = 15 m + 15 m = 30 m
Antwort: Für beide Zimmer müssen sie 35,5 m2 Laminat kaufen und 30 m Fußleisten.
www.Klassenarbeiten.de Seite 8
2. Zwei Straßen sind 5,50 m und 7,50 m breit.
Sie kreuzen sich unter einem Winkel von 60°.
Wie groß ist der Flächeninhalt der Kreuzung?
Fertige eine Zeichnung an.
Amarkierte Fläche: 8,60 m · 5,50 m = 47,30 m²
3. Berechne die Fläche des Dreiecks für
a = 2 cm; h = 3 cm A = 0,5 · 2 cm · 3 cm = 3 cm2
a = 8 cm; h = 5 cm A = 0,5 · 8 cm · 5 cm = 20 cm2
a = 5,5 cm; h = 3 cm A = 0,5 · 5,5 cm · 3 cm = 8,25 cm2
4. Berechne den Umfang eines Dreiecks mit den angegebenen Seitenlängen.
a = 6 cm; b = 3 cm; c = 10cm U = 6 cm + 3 cm + 10 cm = 19 cm
a = 8,2 mm; b = 4,5 mm; c = 13,7 mm U = 8,2 mm + 4,5 mm + 13,7 mm = 26,4 mm
a = 6,8 km; b= 3100 m; c = 211 m U = 6,8 km + 3,1 km + 0,211 km = 10,111 km
5. Der Flächeninhalt eines Trapezes wird aus den Längen der beiden parallelen
Seiten und der Höhe berechnet.
6. Berechne die fehlenden Größen eines Trapezes. Fläche des Trapezes: A = 0,5 ∙ ( a + c) ∙ h
a) b) c) d) e) f)
a 7,6 cm 8 cm 3,2 m 12 dm 14,4 km 4,5 cm
c 3,4 cm 5 cm 1,8 m 8 dm 7,2 km 2,3 cm
h 4 cm 4,2 cm 90 cm 4,8 dm 2,5 km 2,5 cm
A 22 cm2 27,3 cm² 2,25 m² 48 dm2 27 km² 8,5 cm²
a) 0,5 ∙(7,6 cm + 3,4 cm) ∙ 4 cm = 0,5 ∙ 11 cm ∙ 4 cm = 0,5 ∙ 44 cm2 = 22 cm2
b) 0,5 ∙ (8 cm + c cm) ∙ 4,2 cm = 27,3 cm2
(4 cm + 0,5 c cm) ∙ 4,2 cm = 27,3 cm2
16,8 cm2 + 2,1 c = 27,3 cm2 | - 16,8 cm2
2,1 c = 10,5 cm | : 2,1 cm
c = 5 cm
c) 0,5 (x m + 1,8 m) ∙ 0,9 m = 2,25 m2
(0,5 x + 0,9) ∙ 0,9 = 2,25
0,45x + 0,81 =2,25 | - 0,81
0,45x = 1,44 | : 0,45
x = 3,2 cm
d) 0,5 (12 dm + 8 dm) ∙ 4,8 dm = 10 dm ∙ 4,8 dm = 48 dm2
e) 0,5 (14,4 + 7,2) ∙ x = 27
10,8 x = 27 | : 10,8
x = 2,5 km
f) 0,5 (4,5 + x ) ∙ 2,5 = 8,5
(4,5 + x) ∙ 1,25 = 8,5
5,625 + 1,25 x = 8,5 | - 5,625
1,25 x = 2,875
x = 2,3 cm
2. Zwei Straßen sind 5,50 m und 7,50 m breit.
Sie kreuzen sich unter einem Winkel von 60°.
Wie groß ist der Flächeninhalt der Kreuzung?
Fertige eine Zeichnung an.
Amarkierte Fläche: 8,60 m · 5,50 m = 47,30 m²
3. Berechne die Fläche des Dreiecks für
a = 2 cm; h = 3 cm A = 0,5 · 2 cm · 3 cm = 3 cm2
a = 8 cm; h = 5 cm A = 0,5 · 8 cm · 5 cm = 20 cm2
a = 5,5 cm; h = 3 cm A = 0,5 · 5,5 cm · 3 cm = 8,25 cm2
4. Berechne den Umfang eines Dreiecks mit den angegebenen Seitenlängen.
a = 6 cm; b = 3 cm; c = 10cm U = 6 cm + 3 cm + 10 cm = 19 cm
a = 8,2 mm; b = 4,5 mm; c = 13,7 mm U = 8,2 mm + 4,5 mm + 13,7 mm = 26,4 mm
a = 6,8 km; b= 3100 m; c = 211 m U = 6,8 km + 3,1 km + 0,211 km = 10,111 km
5. Der Flächeninhalt eines Trapezes wird aus den Längen der beiden parallelen
Seiten und der Höhe berechnet.
6. Berechne die fehlenden Größen eines Trapezes. Fläche des Trapezes: A = 0,5 ∙ ( a + c) ∙ h
a) b) c) d) e) f)
a 7,6 cm 8 cm 3,2 m 12 dm 14,4 km 4,5 cm
c 3,4 cm 5 cm 1,8 m 8 dm 7,2 km 2,3 cm
h 4 cm 4,2 cm 90 cm 4,8 dm 2,5 km 2,5 cm
A 22 cm2 27,3 cm² 2,25 m² 48 dm2 27 km² 8,5 cm²
a) 0,5 ∙(7,6 cm + 3,4 cm) ∙ 4 cm = 0,5 ∙ 11 cm ∙ 4 cm = 0,5 ∙ 44 cm2 = 22 cm2
b) 0,5 ∙ (8 cm + c cm) ∙ 4,2 cm = 27,3 cm2
(4 cm + 0,5 c cm) ∙ 4,2 cm = 27,3 cm2
16,8 cm2 + 2,1 c = 27,3 cm2 | - 16,8 cm2
2,1 c = 10,5 cm | : 2,1 cm
c = 5 cm
c) 0,5 (x m + 1,8 m) ∙ 0,9 m = 2,25 m2
(0,5 x + 0,9) ∙ 0,9 = 2,25
0,45x + 0,81 =2,25 | - 0,81
0,45x = 1,44 | : 0,45
x = 3,2 cm
d) 0,5 (12 dm + 8 dm) ∙ 4,8 dm = 10 dm ∙ 4,8 dm = 48 dm2
e) 0,5 (14,4 + 7,2) ∙ x = 27
10,8 x = 27 | : 10,8
x = 2,5 km
f) 0,5 (4,5 + x ) ∙ 2,5 = 8,5
(4,5 + x) ∙ 1,25 = 8,5
5,625 + 1,25 x = 8,5 | - 5,625
1,25 x = 2,875
x = 2,3 cm
www.Klassenarbeiten.de Seite 9
7. Zeichne die Punkte in ein Koordinatensystem und verbinde sie. Berechne den
Flächeninhalt der Vierecke ABCD.
a) A(1/0); B(4,5/0); C(4,5/3); D(1/3,5) b) A(4/0); B(6/3); C(3/7); D(1/3)
Trapez A=a + c
2 ∙h= Es entsteht ein Viereck, das aus 4-recht-
3 + 3,5
2 ∙3,5=11,375 cm² winkligen Dreiecken zusammengesetzt
ist. Man erhält:
A=2 ∙ 4
2 +4 ∙ 3
2 +3 ∙ 3
2 +3 ∙ 2
2
A=4+6+4,5+3=17,5 cm²
c) A(-2,5/-2); B(-1/0); C(-2,5/2); D(-4/0) d) A(1/1); B(4/6); C(8/1); D(5/3)
Raute A=e ∙ f
2 =3 ∙ 4
2 =6 cm² A=AABC −AACD A=7 ∙ 5
2 −7 ∙ 2
2 =10,5 cm²
Flächeninhalt und Umfang Lösung 8. Klasse 3
1. Zeichne das Parallelogramm ABCD mit A(4|1), B(7|1), C(3|5) und D(0|5) in ein
Koordinatensystem.
a) Bestimme den Flächeninhalt in cm²
Als Grundlinie wählt man die Strecke 𝐴𝐵̅̅̅̅ = 3cm,
die Höhe beträgt 4 cm.
A = g ∙ h = 3 cm ∙ 4 cm = 12 cm2
b) Berechne den Umfang
Beim Umfang ist die Strecke 𝐴𝐷̅̅̅̅ abzumessen.
(oder man rechnet sie mit Pythagoras aus:
𝐴𝐷̅̅̅̅ = √42 +42 = √32=5,66 )
U = 2 · (3 cm + 5,7 cm) = 17,4 cm
c) Berechne die Höhe hB (runde)
A=g∙h; h= A
g ; hb = 12 cm2 : 5,7 cm = 2,1 cm
d) Trage den Punkt E(1,5|2,5) ein. Verbinde ihn mit C und A. Wo muss F liegen, damit
daraus die Raute EAFC entsteht? F (5,5|3,5)
2. Berechne den Flächeninhalt der folgenden Dreiecke.
a = 7,4 cm; ha = 3,6 cm A=a ∙ ha
2 =7,4 ∙ 3,6
2 =13,32 cm²
c = 70,4 m; hc = 44,8 m A=c ∙ hc
2 =70,4 ∙ 44,8
2 =1576,96 m²
7. Zeichne die Punkte in ein Koordinatensystem und verbinde sie. Berechne den
Flächeninhalt der Vierecke ABCD.
a) A(1/0); B(4,5/0); C(4,5/3); D(1/3,5) b) A(4/0); B(6/3); C(3/7); D(1/3)
Trapez A=a + c
2 ∙h= Es entsteht ein Viereck, das aus 4-recht-
3 + 3,5
2 ∙3,5=11,375 cm² winkligen Dreiecken zusammengesetzt
ist. Man erhält:
A=2 ∙ 4
2 +4 ∙ 3
2 +3 ∙ 3
2 +3 ∙ 2
2
A=4+6+4,5+3=17,5 cm²
c) A(-2,5/-2); B(-1/0); C(-2,5/2); D(-4/0) d) A(1/1); B(4/6); C(8/1); D(5/3)
Raute A=e ∙ f
2 =3 ∙ 4
2 =6 cm² A=AABC −AACD A=7 ∙ 5
2 −7 ∙ 2
2 =10,5 cm²
Flächeninhalt und Umfang Lösung 8. Klasse 3
1. Zeichne das Parallelogramm ABCD mit A(4|1), B(7|1), C(3|5) und D(0|5) in ein
Koordinatensystem.
a) Bestimme den Flächeninhalt in cm²
Als Grundlinie wählt man die Strecke 𝐴𝐵̅̅̅̅ = 3cm,
die Höhe beträgt 4 cm.
A = g ∙ h = 3 cm ∙ 4 cm = 12 cm2
b) Berechne den Umfang
Beim Umfang ist die Strecke 𝐴𝐷̅̅̅̅ abzumessen.
(oder man rechnet sie mit Pythagoras aus:
𝐴𝐷̅̅̅̅ = √42 +42 = √32=5,66 )
U = 2 · (3 cm + 5,7 cm) = 17,4 cm
c) Berechne die Höhe hB (runde)
A=g∙h; h= A
g ; hb = 12 cm2 : 5,7 cm = 2,1 cm
d) Trage den Punkt E(1,5|2,5) ein. Verbinde ihn mit C und A. Wo muss F liegen, damit
daraus die Raute EAFC entsteht? F (5,5|3,5)
2. Berechne den Flächeninhalt der folgenden Dreiecke.
a = 7,4 cm; ha = 3,6 cm A=a ∙ ha
2 =7,4 ∙ 3,6
2 =13,32 cm²
c = 70,4 m; hc = 44,8 m A=c ∙ hc
2 =70,4 ∙ 44,8
2 =1576,96 m²
www.Klassenarbeiten.de Seite 10
7.50 cm
3.80 cm
3.45 cm 4.50 cm
50.0 ° 9.50 cm
4.00 cm
8.60 cm 110.0 °
3.62 cm
6.48 cm 5.60 cm
5.50 cm
54.0 °
5.37 cm
4.70 cm
b = 12,3 dm; hb = 88 cm A=b ∙ hb
2 =12,3 ∙ 8,8
2 =54,12 dm²
a = 6,4 cm; ha = 3,6 cm A=a ∙ ha
2 =6,4 ∙ 3,6
2 =11,52 cm²
3. Zeichne die folgenden Trapeze und berechne ihren Flächeninhalt.
a) a = 7,5 cm; b = 4,5 cm; c = 3,8 cm; ß = 50°
A=a + c
2 ∙h=7,5 + 3,8
2 ∙3,45≈19,49 cm²
b) a = 9,5 cm; b = 4 cm; e = 8,6 cm; = 110°
A=a + c
2 ∙h=9,5 + 6,48
2 ∙3,6≈28,76 cm²
c) a = 5,5 cm; c = 4,7 cm; e = 5,6 cm; ß = 54°
A=a + c
2 ∙h=5,5 + 4,7
2 ∙5,37≈27,39 cm²
a) b)
c)
4. Berechne die gesuchte Länge.
Rechteck A = 240 cm²; b = 30 cm; a = ? a=A
b =240 cm2
30 cm =8 cm
Dreieck A = 48 cm²; g = 10 cm; h = ? A=2 ∙ A
g =2 ∙ 48 cm2
10 cm =9,6 cm
Parallelogramm U = 124 m; a = 42 m; b = ?
U=2a+2b→b=U−2a
2 =124 m − 2 ∙ 42 m
2 =20m
Parallelogramm A = 96 cm²; h = 6 cm; g = ? A=g∙h→g=A
h =96 cm2
6 cm =16 cm
Trapez A = 630 cm²; h = 30 cm; a = 7 cm; c = ?
A=a+c
2 ∙h→c=2A
h −a=2 ∙ 630 cm2
30 cm −7 cm=35 cm
Trapez A = 360 cm²; a = 6 cm; c = 3 cm; h = ?
A=a+c
2 ∙h→h= 2A
a+c = 2 ∙ 360 cm2
6 cm + 3 cm =720 cm2
9 cm =80 cm
7.50 cm
3.80 cm
3.45 cm 4.50 cm
50.0 ° 9.50 cm
4.00 cm
8.60 cm 110.0 °
3.62 cm
6.48 cm 5.60 cm
5.50 cm
54.0 °
5.37 cm
4.70 cm
b = 12,3 dm; hb = 88 cm A=b ∙ hb
2 =12,3 ∙ 8,8
2 =54,12 dm²
a = 6,4 cm; ha = 3,6 cm A=a ∙ ha
2 =6,4 ∙ 3,6
2 =11,52 cm²
3. Zeichne die folgenden Trapeze und berechne ihren Flächeninhalt.
a) a = 7,5 cm; b = 4,5 cm; c = 3,8 cm; ß = 50°
A=a + c
2 ∙h=7,5 + 3,8
2 ∙3,45≈19,49 cm²
b) a = 9,5 cm; b = 4 cm; e = 8,6 cm; = 110°
A=a + c
2 ∙h=9,5 + 6,48
2 ∙3,6≈28,76 cm²
c) a = 5,5 cm; c = 4,7 cm; e = 5,6 cm; ß = 54°
A=a + c
2 ∙h=5,5 + 4,7
2 ∙5,37≈27,39 cm²
a) b)
c)
4. Berechne die gesuchte Länge.
Rechteck A = 240 cm²; b = 30 cm; a = ? a=A
b =240 cm2
30 cm =8 cm
Dreieck A = 48 cm²; g = 10 cm; h = ? A=2 ∙ A
g =2 ∙ 48 cm2
10 cm =9,6 cm
Parallelogramm U = 124 m; a = 42 m; b = ?
U=2a+2b→b=U−2a
2 =124 m − 2 ∙ 42 m
2 =20m
Parallelogramm A = 96 cm²; h = 6 cm; g = ? A=g∙h→g=A
h =96 cm2
6 cm =16 cm
Trapez A = 630 cm²; h = 30 cm; a = 7 cm; c = ?
A=a+c
2 ∙h→c=2A
h −a=2 ∙ 630 cm2
30 cm −7 cm=35 cm
Trapez A = 360 cm²; a = 6 cm; c = 3 cm; h = ?
A=a+c
2 ∙h→h= 2A
a+c = 2 ∙ 360 cm2
6 cm + 3 cm =720 cm2
9 cm =80 cm
www.Klassenarbeiten.de Seite 11
5. Bestimme den Flächeninhalt der Figuren durch geschickte Zerlegung. Zeichne
diese ein und notiere die Flächeninhalte der Teilflächen in der Zeichnung.
A = 6 cm² A = 4 cm²
6. Berechne die folgenden Giebelflächen.
a) Ages = ATrapez + ADreieck Ages = ADreieck + ATrapez
Ages =8,6 m + 6 m
2 ∙5 m+6 m ∙ (6,5 m −5 m)
2 Ages =5,5 m ∙ 8 m
2 +4,6 m + 8 m
2 ∙5,5 m
Ages =14,6 m
2 ∙5 m+6 m ∙ 1,5 m
2 Ages =5,5 m∙4 m +6,3 m∙5,5 m
Ages =7,3 m∙5 m+3 m∙1,5 m Ages =22 m²+34,65 m²
Ages =36,5 m2 + 4,5 m2 Ages =56,65 m²
Ages =41 m2
Flächeninhalt und Umfang Lösung 8. Klasse 4
1. Berechne aus dem Flächeninhalt eines Dreiecks und der Länge einer Seite die
zugehörige Höhe. (ADreieck = c ∙ hc
2 =>hc = 2 ∙ A
c )
A = 18,9 cm²; c = 7 cm hc =2 ∙ A
c =2 ∙ 18,9 cm2
7 cm =5,4 cm
A = 13,5 cm²; a = 4,5 cm ha =2 ∙ A
a =2 ∙ 13,5cm2
4,5 cm =6 cm
A = 32,2 cm²; b = 14 cm hb =2 ∙ A
b =2 ∙ 32,2cm2
14 cm =4,6 cm
A = 49,5 cm; c = 15 cm hc =2 ∙ A
c =2 ∙ 49,5cm2
15 cm =6,6 cm
2. Berechne die fehlenden Größen eines Drachen.
(ADrachen = e ∙ f
2 ) (e= 2 ∙ ADrachen
f ) f= 2 ∙ ADrachen
e
a) b) c) d) e) f)
e 5,2 cm 3,6 cm 10,2 cm 9,3 cm 2,4 dm 27 cm
f 8,4 cm 10 cm 4,2 cm 5,8 cm 6,4 dm 18,4 cm
A 21,84 cm² 18 cm² 21,42 cm² 26,97 cm² 7,68 dm² 248,4 cm²
5. Bestimme den Flächeninhalt der Figuren durch geschickte Zerlegung. Zeichne
diese ein und notiere die Flächeninhalte der Teilflächen in der Zeichnung.
A = 6 cm² A = 4 cm²
6. Berechne die folgenden Giebelflächen.
a) Ages = ATrapez + ADreieck Ages = ADreieck + ATrapez
Ages =8,6 m + 6 m
2 ∙5 m+6 m ∙ (6,5 m −5 m)
2 Ages =5,5 m ∙ 8 m
2 +4,6 m + 8 m
2 ∙5,5 m
Ages =14,6 m
2 ∙5 m+6 m ∙ 1,5 m
2 Ages =5,5 m∙4 m +6,3 m∙5,5 m
Ages =7,3 m∙5 m+3 m∙1,5 m Ages =22 m²+34,65 m²
Ages =36,5 m2 + 4,5 m2 Ages =56,65 m²
Ages =41 m2
Flächeninhalt und Umfang Lösung 8. Klasse 4
1. Berechne aus dem Flächeninhalt eines Dreiecks und der Länge einer Seite die
zugehörige Höhe. (ADreieck = c ∙ hc
2 =>hc = 2 ∙ A
c )
A = 18,9 cm²; c = 7 cm hc =2 ∙ A
c =2 ∙ 18,9 cm2
7 cm =5,4 cm
A = 13,5 cm²; a = 4,5 cm ha =2 ∙ A
a =2 ∙ 13,5cm2
4,5 cm =6 cm
A = 32,2 cm²; b = 14 cm hb =2 ∙ A
b =2 ∙ 32,2cm2
14 cm =4,6 cm
A = 49,5 cm; c = 15 cm hc =2 ∙ A
c =2 ∙ 49,5cm2
15 cm =6,6 cm
2. Berechne die fehlenden Größen eines Drachen.
(ADrachen = e ∙ f
2 ) (e= 2 ∙ ADrachen
f ) f= 2 ∙ ADrachen
e
a) b) c) d) e) f)
e 5,2 cm 3,6 cm 10,2 cm 9,3 cm 2,4 dm 27 cm
f 8,4 cm 10 cm 4,2 cm 5,8 cm 6,4 dm 18,4 cm
A 21,84 cm² 18 cm² 21,42 cm² 26,97 cm² 7,68 dm² 248,4 cm²
www.Klassenarbeiten.de Seite 12
a) ADrachen = 5,2 cm ∙ 8,4 cm
2 = 43,68 cm2
2 =21,84 cm2
b) f= 2 ∙ ADrachen
e = 2 ∙ 18 cm2
3,6 cm = 10 cm
c) e= 2 ∙ ADrachen
f = 2 ∙ 21,42 cm2
4,2 cm = 10,2 cm
d) ADrachen = 9,3 cm ∙ 5,8 cm
2 = 53,94 cm2
2 =26,97 cm2
e) f= 2 ∙ ADrachen
e = 2 ∙ 7,68 dm2
2,4 dm = 6,4 dm
f) e= 2 ∙ ADrachen
f = 2 ∙ 248,4 cm2
18,4 cm = 27 cm
3. Bestimme den Flächeninhalt der Figuren durch geschickte Ergänzung. Notiere
die Flächeninhalte der Teilflächen in der Zeichnung.
A = 5,75 cm² A = 3,75 cm²
4. Berechne den Flächeninhalt des Fünfecks ABCDE
a) A(3/1); B(8/1); C(6/5); D(7/8); E(1/5)
A ges = A Parallelogramm ABCE +A CDE
A ges = 5 · 4 + 5 ∙ 3
2 =27,5 cm²
b) A(3/0); B(8/2); C(7/6); D(3/8); E(1/4)
Ages = AADE + ACDX + AABY + ATrBCXY
Ages = 8 ∙ 2
2 +4 ∙ 2
2 +5 ∙ 2
2 +8 + 4
2 ∙4
Ages = 8 + 4 + 5 + 18
Ages = 36,25 cm²
5. Wie groß ist der Flächeninhalt eines Quadrates mit der Diagonalen e = 6 cm?
Ein Quadrat ist ein spezieller Drachen mit e = f
A=e ∙f
2 =6 ∙ 6
2 =18 cm²
6. Konstruiere einen Drachen aus den gegebenen Größen. Entnimm die fehlenden
Maße der Zeichnung und berechne den Flächeninhalt.
a) a = 6 cm; d = 4 cm; f = 7,6 cm A ≈7,6 ∙ 6,3
2 ≈23,94 cm²
b) b = 5 cm; c = 3,6 cm; = 1300 A ≈3,5 ∙ 7,8
2 ≈13,65 cm²
Fläche des Rechtecks:
2,5 cm ∙ 3,5 cm = 8,75 cm2
a) Zu berechnende Fläche:
8,75 cm2 – 4∙ 3
4 cm2 = 5,75 cm2
b) 8,75 cm2 – 5 cm2 = 3,75 cm2
a) ADrachen = 5,2 cm ∙ 8,4 cm
2 = 43,68 cm2
2 =21,84 cm2
b) f= 2 ∙ ADrachen
e = 2 ∙ 18 cm2
3,6 cm = 10 cm
c) e= 2 ∙ ADrachen
f = 2 ∙ 21,42 cm2
4,2 cm = 10,2 cm
d) ADrachen = 9,3 cm ∙ 5,8 cm
2 = 53,94 cm2
2 =26,97 cm2
e) f= 2 ∙ ADrachen
e = 2 ∙ 7,68 dm2
2,4 dm = 6,4 dm
f) e= 2 ∙ ADrachen
f = 2 ∙ 248,4 cm2
18,4 cm = 27 cm
3. Bestimme den Flächeninhalt der Figuren durch geschickte Ergänzung. Notiere
die Flächeninhalte der Teilflächen in der Zeichnung.
A = 5,75 cm² A = 3,75 cm²
4. Berechne den Flächeninhalt des Fünfecks ABCDE
a) A(3/1); B(8/1); C(6/5); D(7/8); E(1/5)
A ges = A Parallelogramm ABCE +A CDE
A ges = 5 · 4 + 5 ∙ 3
2 =27,5 cm²
b) A(3/0); B(8/2); C(7/6); D(3/8); E(1/4)
Ages = AADE + ACDX + AABY + ATrBCXY
Ages = 8 ∙ 2
2 +4 ∙ 2
2 +5 ∙ 2
2 +8 + 4
2 ∙4
Ages = 8 + 4 + 5 + 18
Ages = 36,25 cm²
5. Wie groß ist der Flächeninhalt eines Quadrates mit der Diagonalen e = 6 cm?
Ein Quadrat ist ein spezieller Drachen mit e = f
A=e ∙f
2 =6 ∙ 6
2 =18 cm²
6. Konstruiere einen Drachen aus den gegebenen Größen. Entnimm die fehlenden
Maße der Zeichnung und berechne den Flächeninhalt.
a) a = 6 cm; d = 4 cm; f = 7,6 cm A ≈7,6 ∙ 6,3
2 ≈23,94 cm²
b) b = 5 cm; c = 3,6 cm; = 1300 A ≈3,5 ∙ 7,8
2 ≈13,65 cm²
Fläche des Rechtecks:
2,5 cm ∙ 3,5 cm = 8,75 cm2
a) Zu berechnende Fläche:
8,75 cm2 – 4∙ 3
4 cm2 = 5,75 cm2
b) 8,75 cm2 – 5 cm2 = 3,75 cm2
www.Klassenarbeiten.de Seite 13
7.60 cm
6.00 cm
4.00 cm 6.27 cm
a) b)
7. Berechne die fehlenden Größen eines
Parallelogramms.
a) b) c) d) e) f)
g 4,4 cm 5,4 cm 24 dm 40 cm 5,5 m 6 km
h 2,2 cm ca. 3,3 cm 35 dm 60 cm 17,5 m 3,2 km
A 9,68 cm² 17,6 cm² 8,4 m² 2 400 cm² 96,25 m² 19,2 km²
Fläche des Parallelogramms: A = g ∙ h, Grundlinie: g= A
h ; Höhe: h= A
g
a) A = 4,4 cm ∙ 2,2 cm =9,68 cm2
b) h= A
g; h= 17,6 cm2
5,4 cm =3,259̅̅̅̅̅cm
c) 8,4 m2 = 840 dm2; g= A
h; g= 840 dm2
35 dm = 24 dm
d) A = 40 cm ∙ 60 cm = 2400 cm2
e) h= A
g; h= 96,25 cm2
5,5 cm =17,5 cm
f) g= A
h; g= 19,2 km2
3,2 km = 6 km
7.82 cm
3.53 cm
5.00 cm
3.60 cm
130.0 °
7.60 cm
6.00 cm
4.00 cm 6.27 cm
a) b)
7. Berechne die fehlenden Größen eines
Parallelogramms.
a) b) c) d) e) f)
g 4,4 cm 5,4 cm 24 dm 40 cm 5,5 m 6 km
h 2,2 cm ca. 3,3 cm 35 dm 60 cm 17,5 m 3,2 km
A 9,68 cm² 17,6 cm² 8,4 m² 2 400 cm² 96,25 m² 19,2 km²
Fläche des Parallelogramms: A = g ∙ h, Grundlinie: g= A
h ; Höhe: h= A
g
a) A = 4,4 cm ∙ 2,2 cm =9,68 cm2
b) h= A
g; h= 17,6 cm2
5,4 cm =3,259̅̅̅̅̅cm
c) 8,4 m2 = 840 dm2; g= A
h; g= 840 dm2
35 dm = 24 dm
d) A = 40 cm ∙ 60 cm = 2400 cm2
e) h= A
g; h= 96,25 cm2
5,5 cm =17,5 cm
f) g= A
h; g= 19,2 km2
3,2 km = 6 km
7.82 cm
3.53 cm
5.00 cm
3.60 cm
130.0 °
www.Klassenarbeiten.de Seite 14
7.60 cm
3.00 cm
2.80 cm
7.09 cm
Flächeninhalt und Umfang Lösung 8. Klasse 5
1. Konstruiere ein Dreieck aus a = 5,6 cm; b = 4,8 cm und c = 6,2 cm. Zeichne in das
Dreieck die drei Höhen ein und berechne dreimal aus einer Seite und der
dazugehörigen Höhe den Flächeninhalt.
A1 =a ∙ ha
2 =5,6 ∙ 4,58
2 =12,824 cm²
A2 =b ∙ hb
2 =4,8 ∙ 5,35
2 =12,84 cm²
A3 =c ∙ hc
2 =6,2 ∙ 4,14
2 =12,834 cm²
2. Berechne die fehlende Größe des Trapezes
A = 216 cm²; h = 8 cm; c = 24 cm; a = ?
A=a + c
2 ∙h→2 ∙ A
h =a+c→2 ∙ A
h −c=a 2 ∙ 216 cm²
8 cm −24 cm=30 cm
A = 810 m²; h = 18 m; a = 53 m; c = ?
A=a + c
2 ∙h→2 ∙ A
h =a+c→2 ∙ A
h −a=c 2 ∙ 810 m²
18 m −53 m=37 m
3. Ein Haus soll verklinkert werden. Wie groß ist die Fläche, wenn für Fenster und
Türen 22% der Gesamtfläche abgerechnet werden?
Ages = (2 · 10,4 · 12,2 + 2∙ 14 · 12,2 + 2∙10,4 ∙ 5,2
2 )∙0,78=506,56 m²
4. Berechne den Flächeninhalt der dick umrandeten Fläche
A=2 ∙ 10 ∙4
2 =40 cm²
5. In einem Parallelogramm ist a = 7,6 cm, b = 3 cm, ha = 2,8 cm. Bestimme hb durch
Zeichnung und durch Rechnung.
A = 7,6 cm · 2,8 cm
A = 21,28 cm²
21,28 = 3 · hb
hb = 7,09 cm
10 cm
8 cm
7.60 cm
3.00 cm
2.80 cm
7.09 cm
Flächeninhalt und Umfang Lösung 8. Klasse 5
1. Konstruiere ein Dreieck aus a = 5,6 cm; b = 4,8 cm und c = 6,2 cm. Zeichne in das
Dreieck die drei Höhen ein und berechne dreimal aus einer Seite und der
dazugehörigen Höhe den Flächeninhalt.
A1 =a ∙ ha
2 =5,6 ∙ 4,58
2 =12,824 cm²
A2 =b ∙ hb
2 =4,8 ∙ 5,35
2 =12,84 cm²
A3 =c ∙ hc
2 =6,2 ∙ 4,14
2 =12,834 cm²
2. Berechne die fehlende Größe des Trapezes
A = 216 cm²; h = 8 cm; c = 24 cm; a = ?
A=a + c
2 ∙h→2 ∙ A
h =a+c→2 ∙ A
h −c=a 2 ∙ 216 cm²
8 cm −24 cm=30 cm
A = 810 m²; h = 18 m; a = 53 m; c = ?
A=a + c
2 ∙h→2 ∙ A
h =a+c→2 ∙ A
h −a=c 2 ∙ 810 m²
18 m −53 m=37 m
3. Ein Haus soll verklinkert werden. Wie groß ist die Fläche, wenn für Fenster und
Türen 22% der Gesamtfläche abgerechnet werden?
Ages = (2 · 10,4 · 12,2 + 2∙ 14 · 12,2 + 2∙10,4 ∙ 5,2
2 )∙0,78=506,56 m²
4. Berechne den Flächeninhalt der dick umrandeten Fläche
A=2 ∙ 10 ∙4
2 =40 cm²
5. In einem Parallelogramm ist a = 7,6 cm, b = 3 cm, ha = 2,8 cm. Bestimme hb durch
Zeichnung und durch Rechnung.
A = 7,6 cm · 2,8 cm
A = 21,28 cm²
21,28 = 3 · hb
hb = 7,09 cm
10 cm
8 cm