www.Klassenarbeiten.de Seite 1
Berechnung von Körpervolumen Station 1
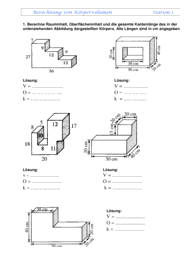
1. Berechne Rauminhalt, Oberflächeninhalt und die gesamte Kantenlänge des in der
untenstehenden Abbildung dargestellten Körpers. Alle Längen sind in cm angegeben.
Lösung: Lösung:
V = ........................ V = ...................
O = .................. O = ..............
k = ....................... k = ..................
Lösung: Lösung:
V = ....................... V = .......................
O = ....................... O = .......................
k = ....................... k = .......................
Lösung:
V = .......................
O = .......................
k = .......................
Berechnung von Körpervolumen Station 1
1. Berechne Rauminhalt, Oberflächeninhalt und die gesamte Kantenlänge des in der
untenstehenden Abbildung dargestellten Körpers. Alle Längen sind in cm angegeben.
Lösung: Lösung:
V = ........................ V = ...................
O = .................. O = ..............
k = ....................... k = ..................
Lösung: Lösung:
V = ....................... V = .......................
O = ....................... O = .......................
k = ....................... k = .......................
Lösung:
V = .......................
O = .......................
k = .......................
www.Klassenarbeiten.de Seite 2
Berechnung von Körpervolumen Station 2
1. Berechne Rauminhalt, Oberflächeninhalt und die gesamte Kantenlänge des in der
untenstehenden Abbildung dargestellten Körpers. Alle Längen sind in cm angegeben.
Fertige gegebenenfalls vor Beginn jeder Aufgabe eine kleine Skizze an . Vergiss nicht,
eventuelle Zwischenschritte zu kommentieren und achte auf den richtigen Gebrauch
der Maßeinheiten.
2. Ein Lastwagen mit einer Ladefläche von 3,00m x 1,80m ist 40cm hoch mit Sand beladen.
Wie viel m3 Sand sind auf dem Lastwagen?
Antwort: ___________________________
3. Im Schwimmbad ist das große Becken 50 m lang und 20 m breit, die Wassertiefe beträgt
2,40m. Wie viel m3 Wasser sind in dem Becken?
Antwort: ___________________________
Lösung:
V = .......................
O = .......................
k = .......................
Lösung:
V = .......................
O = .......................
k = .......................
Lösung:
V = .......................
O = .......................
k = .......................
Berechnung von Körpervolumen Station 2
1. Berechne Rauminhalt, Oberflächeninhalt und die gesamte Kantenlänge des in der
untenstehenden Abbildung dargestellten Körpers. Alle Längen sind in cm angegeben.
Fertige gegebenenfalls vor Beginn jeder Aufgabe eine kleine Skizze an . Vergiss nicht,
eventuelle Zwischenschritte zu kommentieren und achte auf den richtigen Gebrauch
der Maßeinheiten.
2. Ein Lastwagen mit einer Ladefläche von 3,00m x 1,80m ist 40cm hoch mit Sand beladen.
Wie viel m3 Sand sind auf dem Lastwagen?
Antwort: ___________________________
3. Im Schwimmbad ist das große Becken 50 m lang und 20 m breit, die Wassertiefe beträgt
2,40m. Wie viel m3 Wasser sind in dem Becken?
Antwort: ___________________________
Lösung:
V = .......................
O = .......................
k = .......................
Lösung:
V = .......................
O = .......................
k = .......................
Lösung:
V = .......................
O = .......................
k = .......................
www.Klassenarbeiten.de Seite 3
Berechnung von Körpervolumen Station 3
1. In ein Schwimmbecken, das 20 m lang und 15 m breit ist, werden 360 000 Liter
gegossen. Wie hoch steht das Wasser?
Antwort: ___________________________
2. Berechne das Volumen des Trägers.
3. Berechne Volumen und Oberflächeninhalt des linken Körper (links Maße in mm) und das
Volumen des rechten Körpers.
4. Berechne die Oberfläche und das Volumen der folgenden Körper:
5. In einem Aquarium, das 40 cm lang, 28 cm breit und 35 cm hoch ist, werden 18 Liter
Wasser eingefüllt. Wie hoch steht das Wasser im Aquarium.
Berechnung von Körpervolumen Station 3
1. In ein Schwimmbecken, das 20 m lang und 15 m breit ist, werden 360 000 Liter
gegossen. Wie hoch steht das Wasser?
Antwort: ___________________________
2. Berechne das Volumen des Trägers.
3. Berechne Volumen und Oberflächeninhalt des linken Körper (links Maße in mm) und das
Volumen des rechten Körpers.
4. Berechne die Oberfläche und das Volumen der folgenden Körper:
5. In einem Aquarium, das 40 cm lang, 28 cm breit und 35 cm hoch ist, werden 18 Liter
Wasser eingefüllt. Wie hoch steht das Wasser im Aquarium.
www.Klassenarbeiten.de Seite 4
Berechnung von Körpervolumen Station 4
1. In einem Park befindet sich ein Blumenbeet inForm einer Raute.
a) Berechne die Fläche des Beetes
b) Es soll neue Blumenerde in einer Schicht von
10 cm eingefüllt werden.
Berechne das Volumen der Erde
c) Ein Sack Blumenerde hat 50 l. Wie viel
Säcke braucht man?
2. Berechne das Volumen und die Oberfläche der abgebildeten Körper.
3. Berechne das Volumen
4. Welches Volumen hat der zusammengesetzten Körper?
Berechnung von Körpervolumen Station 4
1. In einem Park befindet sich ein Blumenbeet inForm einer Raute.
a) Berechne die Fläche des Beetes
b) Es soll neue Blumenerde in einer Schicht von
10 cm eingefüllt werden.
Berechne das Volumen der Erde
c) Ein Sack Blumenerde hat 50 l. Wie viel
Säcke braucht man?
2. Berechne das Volumen und die Oberfläche der abgebildeten Körper.
3. Berechne das Volumen
4. Welches Volumen hat der zusammengesetzten Körper?
www.Klassenarbeiten.de Seite 5
Berechnung von Körpervolumen Station 5
1. Welches Volumen haben die zusammengesetzten Körper?
2. Welche Kantenlänge hat ein Würfel mit dem Volumen
a) V = 27 cm3
b) V = 216 cm3
c) V = 125 cm3
3. Das Becken im städtischen Freibad wird zu Beginn der Freibadsaison wieder gefüllt.
Wie viel Liter Wasser wird für das Becken benötigt, wenn es randvoll werden soll?
4. Berechne die Höhe des Körpers, wenn das Volumen V = 120cm³ beträgt.
Berechnung von Körpervolumen Station 5
1. Welches Volumen haben die zusammengesetzten Körper?
2. Welche Kantenlänge hat ein Würfel mit dem Volumen
a) V = 27 cm3
b) V = 216 cm3
c) V = 125 cm3
3. Das Becken im städtischen Freibad wird zu Beginn der Freibadsaison wieder gefüllt.
Wie viel Liter Wasser wird für das Becken benötigt, wenn es randvoll werden soll?
4. Berechne die Höhe des Körpers, wenn das Volumen V = 120cm³ beträgt.
www.Klassenarbeiten.de Seite 6
Berechnung von Körpervolumen Lösung Station 1
1. Berechne Rauminhalt, Oberflächeninhalt und die gesamte Kantenlänge des in der
untenstehenden Abbildung dargestellten Körpers. Alle Längen sind in cm
angegeben.
Linker Körper:
(Anmerkung: hier wird zuerst das gesamte Körpervolumen ausgerechnet und dann werden
die fehlenden Teile abgezogen. Es sind aber auch andere Rechenwege möglich.)
V = 27 cm ∙ 36 cm ∙ 7 cm – ( 12 cm ∙ 9 cm ∙ 7 cm ) – ( 9 cm + 9 cm ) ∙ 12 cm ∙ 7 cm =
6804 cm3 – 756 cm3 – 1512 cm3 = 4536 cm3
O = 2 ∙ (27 ∙ 7) + 2 ∙ ( 36 ∙ 7 ) + 2 ∙ [ 36 ∙ (27 – 18 ) + (36 – 12 ) ∙ 9 + (36 – 24 ) ∙ 9 ] =
378 + 504 + 2 [ 324 + 216 + 108] =
882 + 2 ∙ 648 = 882 + 1296 = 2178 cm2
k = 2 ∙ ( 36 + 27 + 36 + 27 ) + 8 ∙ 7 = 2 ∙ 126 + 56 = 252 + 56 = 308 cm
Rechter Körper:
(Anmerkung: Hier ist es am einfachsten vom Volumen des gesamten Körpers das „Loch“
abzuziehen.)
V = 50 cm ∙ 20 cm ∙ 40 cm – 30 cm ∙ 20 cm ∙ 20 cm = 40.000 cm3 – 12.000 cm3 =
28.000 cm3
O = 2 ∙ 50 cm ∙ 20 cm + 2 ∙ 20 cm ∙ 40 cm + 2∙ 50 cm ∙ 40 cm + 2 ∙ 20 cm ∙ 20 cm =
2000 cm2 + 1600 cm2 + 4000 cm2 + 800 cm2 = 8400 cm2
k = 4 ∙ 40 cm + 4 ∙ 20 cm + 4 ∙ 50 cm + 4 ∙ 30 cm + 8 ∙ 20 cm =
160 cm + 80 cm + 200 cm + 120 cm + 160 cm = 720 cm
Berechnung von Körpervolumen Lösung Station 1
1. Berechne Rauminhalt, Oberflächeninhalt und die gesamte Kantenlänge des in der
untenstehenden Abbildung dargestellten Körpers. Alle Längen sind in cm
angegeben.
Linker Körper:
(Anmerkung: hier wird zuerst das gesamte Körpervolumen ausgerechnet und dann werden
die fehlenden Teile abgezogen. Es sind aber auch andere Rechenwege möglich.)
V = 27 cm ∙ 36 cm ∙ 7 cm – ( 12 cm ∙ 9 cm ∙ 7 cm ) – ( 9 cm + 9 cm ) ∙ 12 cm ∙ 7 cm =
6804 cm3 – 756 cm3 – 1512 cm3 = 4536 cm3
O = 2 ∙ (27 ∙ 7) + 2 ∙ ( 36 ∙ 7 ) + 2 ∙ [ 36 ∙ (27 – 18 ) + (36 – 12 ) ∙ 9 + (36 – 24 ) ∙ 9 ] =
378 + 504 + 2 [ 324 + 216 + 108] =
882 + 2 ∙ 648 = 882 + 1296 = 2178 cm2
k = 2 ∙ ( 36 + 27 + 36 + 27 ) + 8 ∙ 7 = 2 ∙ 126 + 56 = 252 + 56 = 308 cm
Rechter Körper:
(Anmerkung: Hier ist es am einfachsten vom Volumen des gesamten Körpers das „Loch“
abzuziehen.)
V = 50 cm ∙ 20 cm ∙ 40 cm – 30 cm ∙ 20 cm ∙ 20 cm = 40.000 cm3 – 12.000 cm3 =
28.000 cm3
O = 2 ∙ 50 cm ∙ 20 cm + 2 ∙ 20 cm ∙ 40 cm + 2∙ 50 cm ∙ 40 cm + 2 ∙ 20 cm ∙ 20 cm =
2000 cm2 + 1600 cm2 + 4000 cm2 + 800 cm2 = 8400 cm2
k = 4 ∙ 40 cm + 4 ∙ 20 cm + 4 ∙ 50 cm + 4 ∙ 30 cm + 8 ∙ 20 cm =
160 cm + 80 cm + 200 cm + 120 cm + 160 cm = 720 cm
www.Klassenarbeiten.de Seite 7
Linker Körper:
V = 8 ∙ 5 ∙ 18 + (18 – 10 ) ∙ 8 ∙ 8 + (17 + 11) ∙ 12 ∙ 8 – (5 + 8 +12 – 20) ∙ 11 ∙ 8 =
720 + 512 + 2688 – 440 = 3480 cm3
O = 18 ∙ 8 + 10 ∙ 8 + (17 + 11 – 8) ∙ 8 + (17 + 11) ∙ 8 (alle senkrechten Flächen (grau))
+ 2 ∙ [5 ∙ 18 + 8 ∙ 8 + (20 – 5 – 8 ) ∙ (11 + 17) + ( 12 + 8 + 5 – 20 ) ∙ 17 ] (vorne u hinten)
+ 25 ∙ 8 + 25 ∙ 8 = (oben und unten)
144 + 80 + 160 + 224 + 2 ∙ [ 90 + 64 + 196 + 85 ] + 200 + 200 =
= 608 + 870 + 400 = 1878 cm2
k = 2 ∙ ( 18 + 5 + 10 + 8 + 20 + 12 +17 + 5 + 11 + 20 ) + 10 ∙ 8 =
2 ∙ 126 + 80 = 252 + 80 = 332 cm
Rechter Körper:
V = 50 cm ∙ 20 cm ∙ 20 cm + 20 cm ∙ 20 cm ∙ 35 cm = 20 000 cm3 + 14 000 cm3 =
34 000 cm3
O = 20 cm ∙ 50 cm ∙ 3 + 30 cm ∙ 20 cm + 20 cm ∙ 20 cm + (vorderer Quader)
20 cm ∙ 35 cm ∙ 3 + 20 cm ∙ 20 cm ∙ 2 + 15 cm ∙ 20 cm (hinterer Quader) =
3000 cm2 + 600 cm2 + 800 cm2 + 2100 cm2 + 800 cm2 + 300 cm2 =
7600 cm2
k = 585 cm
Rechnung:
V = 40 m ∙ 70 m ∙ 20 m – 40 m ∙ 20 m ∙ 20 m = 56000 m3 – 16000 m3 = 40000 m3
O = 2 ∙ (40 cm ∙ 70 cm – 20 cm ∙ 40 cm) + 2 ∙ 70 cm ∙ 20 cm + 2 ∙ 40 cm ∙ 20 cm =
2 ∙ ( 2800 cm2 – 800 cm2) + 2800 cm2 + 1600 cm2 = 8400 cm2
k = 560 cm
Berechnung von Körpervolumen Lösung Station 2
1. Berechne Rauminhalt, Oberflächeninhalt und die gesamte Kantenlänge des in der
untenstehenden Abbildung dargestellten Körpers. Alle Längen sind in cm angegeben.
Rechnung:
V = 15 cm ∙ 25 cm ∙ 10 – 10 cm ∙ 10 cm ∙ 8 cm =
3750 cm3 – 800 cm3 = 2950 cm3
O = 2 ∙ 25 ∙15 – 2 ∙ 10 ∙ 8 + 2 ∙ 10 ∙15 + 2 ∙ 25 ∙ 10 +
+ 2 ∙ 10 ∙ 10 + 2 ∙ 10 ∙ 8 =
= 750 cm2 – 160 cm2 + 300 cm2 + 500 cm2 +
200 cm2 + 160 cm2 =
= 1750 cm2
k = 4 ∙ 25 cm + 4 ∙ 15 cm + 4 ∙ 10 cm + 4 ∙ 10 cm +
4 ∙ 8 cm + 4 ∙ 10 cm =
= 100 cm + 60 cm + 40 cm + 40 cm + 32 cm +
40 cm = 312 cm
Linker Körper:
V = 8 ∙ 5 ∙ 18 + (18 – 10 ) ∙ 8 ∙ 8 + (17 + 11) ∙ 12 ∙ 8 – (5 + 8 +12 – 20) ∙ 11 ∙ 8 =
720 + 512 + 2688 – 440 = 3480 cm3
O = 18 ∙ 8 + 10 ∙ 8 + (17 + 11 – 8) ∙ 8 + (17 + 11) ∙ 8 (alle senkrechten Flächen (grau))
+ 2 ∙ [5 ∙ 18 + 8 ∙ 8 + (20 – 5 – 8 ) ∙ (11 + 17) + ( 12 + 8 + 5 – 20 ) ∙ 17 ] (vorne u hinten)
+ 25 ∙ 8 + 25 ∙ 8 = (oben und unten)
144 + 80 + 160 + 224 + 2 ∙ [ 90 + 64 + 196 + 85 ] + 200 + 200 =
= 608 + 870 + 400 = 1878 cm2
k = 2 ∙ ( 18 + 5 + 10 + 8 + 20 + 12 +17 + 5 + 11 + 20 ) + 10 ∙ 8 =
2 ∙ 126 + 80 = 252 + 80 = 332 cm
Rechter Körper:
V = 50 cm ∙ 20 cm ∙ 20 cm + 20 cm ∙ 20 cm ∙ 35 cm = 20 000 cm3 + 14 000 cm3 =
34 000 cm3
O = 20 cm ∙ 50 cm ∙ 3 + 30 cm ∙ 20 cm + 20 cm ∙ 20 cm + (vorderer Quader)
20 cm ∙ 35 cm ∙ 3 + 20 cm ∙ 20 cm ∙ 2 + 15 cm ∙ 20 cm (hinterer Quader) =
3000 cm2 + 600 cm2 + 800 cm2 + 2100 cm2 + 800 cm2 + 300 cm2 =
7600 cm2
k = 585 cm
Rechnung:
V = 40 m ∙ 70 m ∙ 20 m – 40 m ∙ 20 m ∙ 20 m = 56000 m3 – 16000 m3 = 40000 m3
O = 2 ∙ (40 cm ∙ 70 cm – 20 cm ∙ 40 cm) + 2 ∙ 70 cm ∙ 20 cm + 2 ∙ 40 cm ∙ 20 cm =
2 ∙ ( 2800 cm2 – 800 cm2) + 2800 cm2 + 1600 cm2 = 8400 cm2
k = 560 cm
Berechnung von Körpervolumen Lösung Station 2
1. Berechne Rauminhalt, Oberflächeninhalt und die gesamte Kantenlänge des in der
untenstehenden Abbildung dargestellten Körpers. Alle Längen sind in cm angegeben.
Rechnung:
V = 15 cm ∙ 25 cm ∙ 10 – 10 cm ∙ 10 cm ∙ 8 cm =
3750 cm3 – 800 cm3 = 2950 cm3
O = 2 ∙ 25 ∙15 – 2 ∙ 10 ∙ 8 + 2 ∙ 10 ∙15 + 2 ∙ 25 ∙ 10 +
+ 2 ∙ 10 ∙ 10 + 2 ∙ 10 ∙ 8 =
= 750 cm2 – 160 cm2 + 300 cm2 + 500 cm2 +
200 cm2 + 160 cm2 =
= 1750 cm2
k = 4 ∙ 25 cm + 4 ∙ 15 cm + 4 ∙ 10 cm + 4 ∙ 10 cm +
4 ∙ 8 cm + 4 ∙ 10 cm =
= 100 cm + 60 cm + 40 cm + 40 cm + 32 cm +
40 cm = 312 cm
www.Klassenarbeiten.de Seite 8
2. Ein Lastwagen mit einer Ladefläche von 3,00 m x 1,80 m ist 40 cm hoch mit Sand
beladen.
Wie viel m3 Sand sind auf dem Lastwagen?
3,00 m · 1,80 m · 0,40 m = 2,16 m3
3. Im Schwimmbad ist das große Becken 50 m lang und 20 m breit, die Wassertiefe beträgt
2,40m. Wie viel m3 Wasser sind in dem Becken?
50 m · 20m · 2,40 m = 2400 m3
Berechnung von Körpervolumen Lösung Station 3
1. In ein Schwimmbecken, das 20 m lang und 15 m breit ist, werden 360 000 Liter
gegossen. Wie hoch steht das Wasser?
Gegeben: Schwimmbecken: l = 20 m / b = 15 m / Inhalt: 360 000 Liter (= Volumen)
Gesucht: Wasserstandhöhe
(Umrechnung: 20 m = 200 dm, 15 m = 150 dm
Lösung: VQuader = l • b • h = VQuader = 360 000 Liter = 360 000 dm3
360 000 dm3 = 200 dm • 150 dm • h
h = 360000 dm3
200 dm ∙ 150 dm
h = 360000 dm3
30000 dm2 =12dm=1,2 m
Antwort: Das Wasser steht 1,20 m hoch im Becken.
2. Berechne das Volumen des Trägers.
Rechnung:
V = 12 cm ∙ 12 cm ∙ 5 cm = 720 cm3
O = 4 ∙ 12 cm ∙ 5 cm + 2 ∙ 12 cm ∙ 12 cm =
240 cm2 + 288 cm2 = 528 cm2
k = 4 ∙ 12 cm + 4 ∙ 12 cm + 4 ∙ 5 cm =
48 cm + 48 cm + 20 cm = 116 cm
Rechnung:
V = 12 cm ∙ 15 cm ∙ 6 cm = 1080 cm3
O = 2 ∙ 12 cm ∙ 6 cm + 2 ∙ 15 cm ∙ 6 cm + 2 ∙ 15 cm ∙ 12 cm =
144 cm2 + 180 cm2 + 360 cm2 = 684 cm2
k = 4 ∙ 12 cm + 4 ∙ 15 cm + 4 ∙ 6 cm =
48 cm + 60 cm + 24 cm = 132 cm
2. Ein Lastwagen mit einer Ladefläche von 3,00 m x 1,80 m ist 40 cm hoch mit Sand
beladen.
Wie viel m3 Sand sind auf dem Lastwagen?
3,00 m · 1,80 m · 0,40 m = 2,16 m3
3. Im Schwimmbad ist das große Becken 50 m lang und 20 m breit, die Wassertiefe beträgt
2,40m. Wie viel m3 Wasser sind in dem Becken?
50 m · 20m · 2,40 m = 2400 m3
Berechnung von Körpervolumen Lösung Station 3
1. In ein Schwimmbecken, das 20 m lang und 15 m breit ist, werden 360 000 Liter
gegossen. Wie hoch steht das Wasser?
Gegeben: Schwimmbecken: l = 20 m / b = 15 m / Inhalt: 360 000 Liter (= Volumen)
Gesucht: Wasserstandhöhe
(Umrechnung: 20 m = 200 dm, 15 m = 150 dm
Lösung: VQuader = l • b • h = VQuader = 360 000 Liter = 360 000 dm3
360 000 dm3 = 200 dm • 150 dm • h
h = 360000 dm3
200 dm ∙ 150 dm
h = 360000 dm3
30000 dm2 =12dm=1,2 m
Antwort: Das Wasser steht 1,20 m hoch im Becken.
2. Berechne das Volumen des Trägers.
Rechnung:
V = 12 cm ∙ 12 cm ∙ 5 cm = 720 cm3
O = 4 ∙ 12 cm ∙ 5 cm + 2 ∙ 12 cm ∙ 12 cm =
240 cm2 + 288 cm2 = 528 cm2
k = 4 ∙ 12 cm + 4 ∙ 12 cm + 4 ∙ 5 cm =
48 cm + 48 cm + 20 cm = 116 cm
Rechnung:
V = 12 cm ∙ 15 cm ∙ 6 cm = 1080 cm3
O = 2 ∙ 12 cm ∙ 6 cm + 2 ∙ 15 cm ∙ 6 cm + 2 ∙ 15 cm ∙ 12 cm =
144 cm2 + 180 cm2 + 360 cm2 = 684 cm2
k = 4 ∙ 12 cm + 4 ∙ 15 cm + 4 ∙ 6 cm =
48 cm + 60 cm + 24 cm = 132 cm
www.Klassenarbeiten.de Seite 9
Teilvolumen:
1: 1
2 ∙(2 cm+6 cm)∙2 cm∙2000 cm=8 cm∙2000 cm=16000 cm2
2 2 cm · 4 cm ∙ 2000 cm = 16000 cm3
3: 1
2 ∙(4 cm+2 cm)∙1 cm∙2000 cm=6000 cm3
4 u.5: 2 ∙ ( 2 cm ∙ 3 cm ∙ 2000 cm) = 24 000 cm3
Volumen: 16 000 cm3 + 16000 cm3 + 6000 cm3 + 24 000 cm3 = 62 000 cm3
3. Berechne Volumen und Oberflächeninhalt des linken Körpers (links Maße in mm)
und das Volumen des rechten Körpers.
Linker Körper:
V = G ∙ h
G = 65 mm ∙ 55 mm – 30 mm ∙ 50 mm = 3575 mm2 – 1500 mm2 = 2075 mm2
V = G · h = 2075 mm2 · 40 mm = 83000 mm3
O = 2 ∙ 65 mm ∙ 40 mm + 2 ∙ 55 mm ∙ 40 mm + 2 ∙ ( 55 mm ∙ 65 mm – 30 mm ∙ 50 mm) +
2 ∙ 50 mm ∙ 40 mm =
5200 mm2 + 4400 mm2 + 4150 mm2 + 4000 mm2 = 17750 mm2
Rechter Körper:
VPrisma = G ∙ h
G1 = Grundfläche Rechteck: 7 m ∙ 4,5 m = 31,5 m2
G2 = Grundfläche Dreieck: 1,5 m ∙ 7 m ∙ 1
2 = 5,25 m2
G Gesamt = 31,5 m2 + 5,25 m2 = 36,75 m2
VPrisma = 36,75 m2 ∙ 18 m = 661,5 m3
4. Berechne die Oberfläche und das Volumen der folgenden Körper:
a) b) c)
a) O = 4 · (21 · 7) + 6 · (7 · 7) = 4 ∙ 147 + 6 ∙ 49 = 588 + 294 = 882
V = 21 · 7 · 7 + 7 · 7 · 7 = 1372
b) O = 2 · (7 · 6) + 2 · (7 · 2) + 2 · (6 · 2) + 2 · (3 · 2) + 2 ∙ 2 ∙ 2
84 + 28 + 24 + 12 + 8 = 156
V = 7 · 6 · 2 + 3 · 2 · 2 = 84 + 12 = 96
c) O = 2 · (8 · 2) + 2 · (2 · 3) + (6 · 2) + 2 · (8 · 3) + 2 · (3 · 3) = 122
V = 8 · 2 · 3 + 3 · 3 · 2 = 48 + 18 = 66
5. In einem Aquarium, das 40 cm lang, 28 cm breit und 35 cm hoch ist, werden 18 Liter
Wasser eingefüllt. Wie hoch steht das Wasser im Aquarium?
Gegeben: Aquarium: l = 40 cm / b = 28 cm / Inhalt: 18 000 Liter (= Volumen)
Gesucht: Wasserstandhöhe
Lösung: VQuader = l • b • h = VQuader = 18 000 Liter = 18 000 cm³
18 000 cm³ = 40 cm • 28 cm • h
h = 18000 cm3
40 cm ∙ 28 cm
h = 18000 cm3
1120 cm2 =16,07 cm
Antwort: Das Wasser steht 16,07 cm hoch im Aquarium.
Teilvolumen:
1: 1
2 ∙(2 cm+6 cm)∙2 cm∙2000 cm=8 cm∙2000 cm=16000 cm2
2 2 cm · 4 cm ∙ 2000 cm = 16000 cm3
3: 1
2 ∙(4 cm+2 cm)∙1 cm∙2000 cm=6000 cm3
4 u.5: 2 ∙ ( 2 cm ∙ 3 cm ∙ 2000 cm) = 24 000 cm3
Volumen: 16 000 cm3 + 16000 cm3 + 6000 cm3 + 24 000 cm3 = 62 000 cm3
3. Berechne Volumen und Oberflächeninhalt des linken Körpers (links Maße in mm)
und das Volumen des rechten Körpers.
Linker Körper:
V = G ∙ h
G = 65 mm ∙ 55 mm – 30 mm ∙ 50 mm = 3575 mm2 – 1500 mm2 = 2075 mm2
V = G · h = 2075 mm2 · 40 mm = 83000 mm3
O = 2 ∙ 65 mm ∙ 40 mm + 2 ∙ 55 mm ∙ 40 mm + 2 ∙ ( 55 mm ∙ 65 mm – 30 mm ∙ 50 mm) +
2 ∙ 50 mm ∙ 40 mm =
5200 mm2 + 4400 mm2 + 4150 mm2 + 4000 mm2 = 17750 mm2
Rechter Körper:
VPrisma = G ∙ h
G1 = Grundfläche Rechteck: 7 m ∙ 4,5 m = 31,5 m2
G2 = Grundfläche Dreieck: 1,5 m ∙ 7 m ∙ 1
2 = 5,25 m2
G Gesamt = 31,5 m2 + 5,25 m2 = 36,75 m2
VPrisma = 36,75 m2 ∙ 18 m = 661,5 m3
4. Berechne die Oberfläche und das Volumen der folgenden Körper:
a) b) c)
a) O = 4 · (21 · 7) + 6 · (7 · 7) = 4 ∙ 147 + 6 ∙ 49 = 588 + 294 = 882
V = 21 · 7 · 7 + 7 · 7 · 7 = 1372
b) O = 2 · (7 · 6) + 2 · (7 · 2) + 2 · (6 · 2) + 2 · (3 · 2) + 2 ∙ 2 ∙ 2
84 + 28 + 24 + 12 + 8 = 156
V = 7 · 6 · 2 + 3 · 2 · 2 = 84 + 12 = 96
c) O = 2 · (8 · 2) + 2 · (2 · 3) + (6 · 2) + 2 · (8 · 3) + 2 · (3 · 3) = 122
V = 8 · 2 · 3 + 3 · 3 · 2 = 48 + 18 = 66
5. In einem Aquarium, das 40 cm lang, 28 cm breit und 35 cm hoch ist, werden 18 Liter
Wasser eingefüllt. Wie hoch steht das Wasser im Aquarium?
Gegeben: Aquarium: l = 40 cm / b = 28 cm / Inhalt: 18 000 Liter (= Volumen)
Gesucht: Wasserstandhöhe
Lösung: VQuader = l • b • h = VQuader = 18 000 Liter = 18 000 cm³
18 000 cm³ = 40 cm • 28 cm • h
h = 18000 cm3
40 cm ∙ 28 cm
h = 18000 cm3
1120 cm2 =16,07 cm
Antwort: Das Wasser steht 16,07 cm hoch im Aquarium.
www.Klassenarbeiten.de Seite 10
Berechnung von Körpervolumen Lösung Station 4
1. In einem Park befindet sich ein Blumenbeet in Form einer Raute.
a) Berechne die Fläche des Beetes
A = (8 m · 6 m) : 2 = 24 m2
b) Es soll neue Blumenerde in einer Schicht von
10 cm eingefüllt werden.
Berechne das Volumen der Erde
V = 24 m2 · 0,1 m = 2,4 m3
c) Ein Sack Blumenerde hat 50 l. Wie viel Säcke braucht man?
Umrechnung: 50 l = 50 dm3 = 0,05 m3
2,4 m3 : 0,05 m3 = 48
Es werden 48 Säcke Blumenerde benötigt.
2. Berechne das Volumen und die Oberfläche der abgebildeten Körper.
a) O = 2 · (3 · 6 + 3 · 5 + 6 · 5) cm2 = 2 ∙ ( 18 + 15 + 30) cm2 = 2 ∙ 63 cm2 = 126 cm2
V = 3 cm · 5 cm · 6 cm = 90 cm3
b) O = 2 · 1
2 · 4 · 3,46 cm2 + (4 cm + 4 cm + 4 cm ) · 5 cm =
13,84 cm2 + 60 cm2 = 73,84 cm2
V = 1
2 · 4 cm · 3,46 cm · 5 cm = 6,92 cm2 ∙ 5 cm = 34,6 cm3
c) O = 2 · 1
2 · (5 cm + 3 cm) · 2 cm + 5 cm · (5 cm + 2 cm + 3 cm + 2,83 cm) =
16 cm2 + 5 ∙ 12,83 = 16 cm2 + 64,15 cm2 = 80,15 cm2
V = 1
2 · (5 cm + 3 cm) ∙ 2 cm · 5 cm = 8 cm2 ∙ 5 cm = 40 cm3
3. Berechne das Volumen
VQuader = 11 m · 6 m · 4 m = 264 m3
VTrapez = ((11 m−2∙3 m)+(11 m−2 ∙ 3,16 m)
2 ∙3 m)∙6 m=
= (5 m + 4,68 m
2 ∙3 m)∙6 m=4,84 m∙ 3 m∙6 m
=87,12 m3
264 m3 – 87,12 m3 = 176,88m3
4. Welches Volumen hat der zusammengesetzten Körper?
Der zusammengesetzte Körper besteht aus
8 Quadern mit a = 4 cm, b = 4 cm und c = 2 cm:
V gesamt = 8 ∙ (4 cm · 4 cm · 2 cm)
V gesamt = 256 cm3
Berechnung von Körpervolumen Lösung Station 4
1. In einem Park befindet sich ein Blumenbeet in Form einer Raute.
a) Berechne die Fläche des Beetes
A = (8 m · 6 m) : 2 = 24 m2
b) Es soll neue Blumenerde in einer Schicht von
10 cm eingefüllt werden.
Berechne das Volumen der Erde
V = 24 m2 · 0,1 m = 2,4 m3
c) Ein Sack Blumenerde hat 50 l. Wie viel Säcke braucht man?
Umrechnung: 50 l = 50 dm3 = 0,05 m3
2,4 m3 : 0,05 m3 = 48
Es werden 48 Säcke Blumenerde benötigt.
2. Berechne das Volumen und die Oberfläche der abgebildeten Körper.
a) O = 2 · (3 · 6 + 3 · 5 + 6 · 5) cm2 = 2 ∙ ( 18 + 15 + 30) cm2 = 2 ∙ 63 cm2 = 126 cm2
V = 3 cm · 5 cm · 6 cm = 90 cm3
b) O = 2 · 1
2 · 4 · 3,46 cm2 + (4 cm + 4 cm + 4 cm ) · 5 cm =
13,84 cm2 + 60 cm2 = 73,84 cm2
V = 1
2 · 4 cm · 3,46 cm · 5 cm = 6,92 cm2 ∙ 5 cm = 34,6 cm3
c) O = 2 · 1
2 · (5 cm + 3 cm) · 2 cm + 5 cm · (5 cm + 2 cm + 3 cm + 2,83 cm) =
16 cm2 + 5 ∙ 12,83 = 16 cm2 + 64,15 cm2 = 80,15 cm2
V = 1
2 · (5 cm + 3 cm) ∙ 2 cm · 5 cm = 8 cm2 ∙ 5 cm = 40 cm3
3. Berechne das Volumen
VQuader = 11 m · 6 m · 4 m = 264 m3
VTrapez = ((11 m−2∙3 m)+(11 m−2 ∙ 3,16 m)
2 ∙3 m)∙6 m=
= (5 m + 4,68 m
2 ∙3 m)∙6 m=4,84 m∙ 3 m∙6 m
=87,12 m3
264 m3 – 87,12 m3 = 176,88m3
4. Welches Volumen hat der zusammengesetzten Körper?
Der zusammengesetzte Körper besteht aus
8 Quadern mit a = 4 cm, b = 4 cm und c = 2 cm:
V gesamt = 8 ∙ (4 cm · 4 cm · 2 cm)
V gesamt = 256 cm3
www.Klassenarbeiten.de Seite 11
Berechnung von Körpervolumen Lösung Station 5
1. Welches Volumen haben die zusammengesetzten Körper?
a) Vges = 2 · (300 · 120 · 50) + 200 · 120 · 50
= 2 ∙ 1800000 + 1200000
Vges = 4800000 mm3 = 4800 cm3
b) Vges = 2 · (120 · 240 · 10) + 10 · 240 · 180 =
= 2 ∙ 288000 + 432000
Vges = 1008000 mm3 = 1008 cm3
2. Welche Kantenlänge hat ein Würfel mit dem Volumen
a) V = 27 cm3 a = 3 cm ➔ 3 cm ∙ 3 cm ∙ 3 cm = 27 cm3
b) V = 216 cm3 a = 6 cm ➔ 6 cm ∙ 6 cm ∙ 6 cm = 216 cm3
c) V = 125 cm3 a = 5 cm ➔ 5 cm ∙ 5 cm ∙ 5 cm = 125 cm3
3. Das Becken im städtischen Freibad wird zu Beginn der Freibadsaison wieder gefüllt.
Wie viel Liter Wasser wird für das Becken benötigt, wenn es randvoll werden soll?
VQu = 25 m · 12 m · 3,5 m
= 1050 m3
VTrap = (6 m + 12 m)
2 ∙1,5 m∙12 m
= 9 m ∙ 1,5 m ∙ 12 m
= 162 m3
VGes = VQu – VTrap
= 1050 m3 – 162 m3
= 888 m3
4. Berechne die Höhe des Körpers, wenn das Volumen V = 120 cm3 beträgt.
AG = 6 · 8
2 = 24 cm2
V = AG · h
120 = 24 · h | : 24
h = 5 cm
Berechnung von Körpervolumen Lösung Station 5
1. Welches Volumen haben die zusammengesetzten Körper?
a) Vges = 2 · (300 · 120 · 50) + 200 · 120 · 50
= 2 ∙ 1800000 + 1200000
Vges = 4800000 mm3 = 4800 cm3
b) Vges = 2 · (120 · 240 · 10) + 10 · 240 · 180 =
= 2 ∙ 288000 + 432000
Vges = 1008000 mm3 = 1008 cm3
2. Welche Kantenlänge hat ein Würfel mit dem Volumen
a) V = 27 cm3 a = 3 cm ➔ 3 cm ∙ 3 cm ∙ 3 cm = 27 cm3
b) V = 216 cm3 a = 6 cm ➔ 6 cm ∙ 6 cm ∙ 6 cm = 216 cm3
c) V = 125 cm3 a = 5 cm ➔ 5 cm ∙ 5 cm ∙ 5 cm = 125 cm3
3. Das Becken im städtischen Freibad wird zu Beginn der Freibadsaison wieder gefüllt.
Wie viel Liter Wasser wird für das Becken benötigt, wenn es randvoll werden soll?
VQu = 25 m · 12 m · 3,5 m
= 1050 m3
VTrap = (6 m + 12 m)
2 ∙1,5 m∙12 m
= 9 m ∙ 1,5 m ∙ 12 m
= 162 m3
VGes = VQu – VTrap
= 1050 m3 – 162 m3
= 888 m3
4. Berechne die Höhe des Körpers, wenn das Volumen V = 120 cm3 beträgt.
AG = 6 · 8
2 = 24 cm2
V = AG · h
120 = 24 · h | : 24
h = 5 cm