Klassenarbeiten kostenlos
5. Klasse / Mathematik
Klassenarbeit - Umfang- Volumen- und Flächenberechnung
Winkel; Konstruieren; Schrägbild; Netz; Flächenmaße; Umfang; Flächeninhalt; Rechteck; Sachaufgaben; Volumenberechnung; Oberfläche; Quadratzahlen; Körper
Winkel, Konstruieren
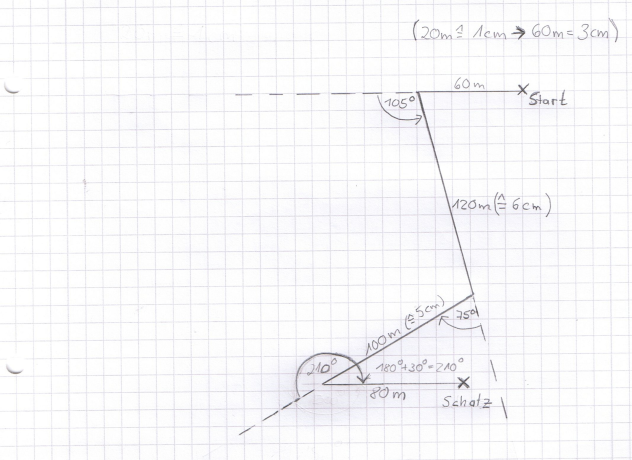
Im Abenteuerurlaub im Ferienheim finden die Kinder folgenden Zettel bei der „Schatzsuche“:
105° nach links und gehe 120 m in dieser Richtung. Wende
dich nun 75° nach rechts und rücke 100m vor. Nach einer
Drehung um 210° nach rechts rücke 80 m vor. Nun liegt der
Schatz vor deinen Füßen!“ (Maßstab: 20 m entsprechen in der Zeichnung 1 cm)
Erstelle eine Schatzkarte!
Im Abenteuerurlaub im Ferienheim finden die Kinder folgenden Zettel bei der „Schatzsuche“:
105° nach links und gehe 120 m in dieser Richtung. Wende
dich nun 75° nach rechts und rücke 100m vor. Nach einer
Drehung um 210° nach rechts rücke 80 m vor. Nun liegt der
Schatz vor deinen Füßen!“ (Maßstab: 20 m entsprechen in der Zeichnung 1 cm)
Erstelle eine Schatzkarte!
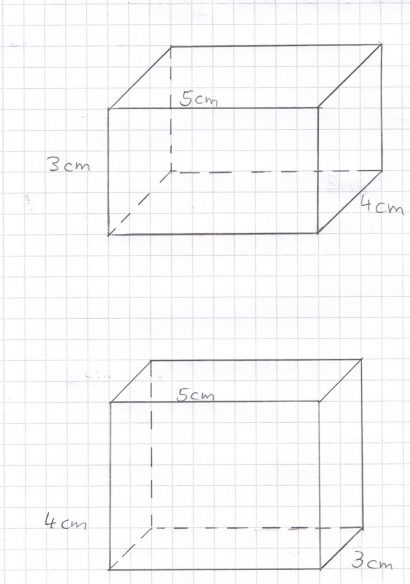
Schrägbild
Zeichne zwei verschiedene Schrägbilder eines Quaders mit den Kantenlängen 3 cm, 4 cm und 5 cm.
Zeichne zwei verschiedene Schrägbilder eines Quaders mit den Kantenlängen 3 cm, 4 cm und 5 cm.
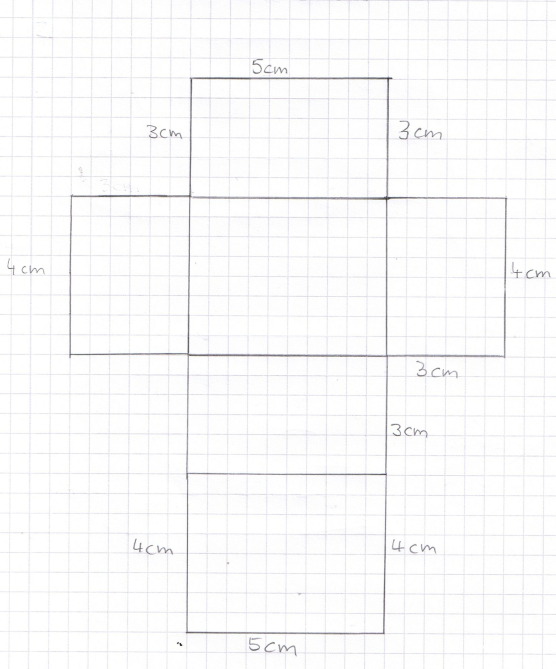
Netz
Zeichne ein Netz eines Quaders mit den Kantenlängen 3 cm, 4 cm und 5 cm.
Zeichne ein Netz eines Quaders mit den Kantenlängen 3 cm, 4 cm und 5 cm.
Flächenmaße
Gib die folgenden Flächenmaße in der Einheit an, die in der Klammer steht:
| a) 7 m² (cm²) | ____________________ | |
| b) 620 ha (a) | ____________________ | |
| c) 4000 dm² (m²) | ____________________ | |
| d) 8ha 24a (a) | ____________________ | |
| e) 900 ha (km²) | ____________________ | |
|
f) 5600 dm² (cm²)
|
____________________ |
Gib die folgenden Flächenmaße in der Einheit an, die in der Klammer steht:
| a) 7 m² (cm²) | 70000 cm² | ( 1 m² = 10000 cm² ) |
| b) 620 ha (a) | 62000 a | ( 1 ha = 100 a ) |
| c) 4000 dm² (m²) | 40 m² | ( 1 dm² = 0,01 m² ) |
| d) 8ha 24a (a) | 824 a | ( 1 ha = 100 a ) |
| e) 900 ha (km²) | 9 km² | ( 1 ha = 0,01 km² ) |
|
f) 5600 dm² (cm²)
|
560000 cm² | ( 1 dm² = 100 cm² ) |
Setze die richtigen Ziffern bzw. Einheiten ein!
Setze die richtigen Ziffern bzw. Einheiten ein!
Umfang, Flächeninhalt, Rechteck
Vervollständige die Tabelle!
| a) | b) | c) | d) | |
| Länge des Rechtecks | 4 cm | 5 cm | 25 m | __________ |
| Breite des Rechtecks | 25 cm | 8 dm | __________ | 150 m |
| Umfang | __________ | __________ | 130 m | 0,38 km |
| Flächeninhalt | __________ | __________ | __________ | __________ |
Vervollständige die Tabelle!
| a) | b) | c) | d) | |
| Länge des Rechtecks | 4 cm | 5 cm | 25 m | 40 m |
| Breite des Rechtecks | 25 cm | 8 dm | 40 m | 150 m |
| Umfang | 58 cm | 170 cm | 10 a | 0,38 km |
| Flächeninhalt | 100 cm² | 400 cm² | 130 m | 6000 m² |
Umfang = 2•Länge + 2•Breite Fläche = Länge • Breite (1a = 100 m²)
a) F: 4 cm ∙ 25 cm = 100 cm2
U: 2∙ 4 cm + 2∙ 25 cm = 8 cm + 50 cm = 58 cm
b) F: 8 dm = 80 cm; 5 cm ∙ 80 cm = 400 cm2
U: 2 ∙ 5 cm + 2 ∙ 80 cm = 10 cm + 160 cm = 170 cm
c) B: 10 a = 1000 m2 ; 1000 m2 : 25 m = 40 m
U: 2 ∙ 25 m + 2 ∙ 40 m = 50 m + 80 m = 130 m
d) L: 0,38 km = 380 m; ( 380 m – 2 ∙ 150 m ) : 2 = 80 m : 2 = 40 m
F: 40 m ∙ 150 m = 6000 m2
Sachaufgaben
Ein Heimwerker will die sechs Türen seiner Wohnung neu streichen.
Alle Türen sind 2 m hoch und 82 cm breit. Eine Farbdose reicht für ca. 12 m².
Wie viele Dosen muss er kaufen, wenn die Türen innen und außen gestrichen werden sollen?
Ein Heimwerker will die sechs Türen seiner Wohnung neu streichen.
Alle Türen sind 2 m hoch und 82 cm breit. Eine Farbdose reicht für ca. 12 m².
Wie viele Dosen muss er kaufen, wenn die Türen innen und außen gestrichen werden sollen?
Volumenberechnung, Oberfläche
Gegeben ist ein Quader mit den Maßen 5 dm, 30 cm und 200 mm.
a) Berechne den Oberflächeninhalt des Quaders und gib das Ergebnis in m² an!
b) Berechne das Volumen eines Quaders und gib das Ergebnis in m³ an!
Gegeben ist ein Quader mit den Maßen 5 dm, 30 cm und 200 mm.
a) Berechne den Oberflächeninhalt des Quaders und gib das Ergebnis in m² an!
b) Berechne das Volumen eines Quaders und gib das Ergebnis in m³ an!
Volumenberechnung
Gib die folgenden Volumenangaben in der Einheit an, die in der Klammer steht.
| a) 320 l (ml) | ____________________ | |
| b) 42000 cm³ (m³) | ____________________ | |
| c) 6250000 mm³ (dm³) | ____________________ | |
| d) 3,02 m³ (dm³) | ____________________ | |
| e) 0,2 l (mm³) | ____________________ | |
|
f) 1,7 m³ (hl)
|
____________________ |
Gib die folgenden Volumenangaben in der Einheit an, die in der Klammer steht.
| a) 320 l (ml) | 320000 ml | ( 1 l = 1000 ml ) |
| b) 42000 cm³ (m³) | 0,042 m³ | ( 1000000 cm³ = 1 m³ ) |
| c) 6250000 mm³ (dm³) | 6,25 dm³ | ( 1000000 mm³ = 1 dm³ ) |
| d) 3,02 m³ (dm³) | 3020 dm³ | ( 1 m³ = 1000 dm³ ) |
| e) 0,2 l (mm³) | 200000 mm³ | ( 1 l = 1000 cm3 = 1000000 mm³ ) |
|
f) 1,7 m³ (hl)
|
1700 l = 17 hl | ( 1 l = 0,01 hl 1hl = 100 l ) |
Quadratzahlen
Gib die Quadratzahlen an!
| a) | 16² = |
| b) | 19² = |
| c) | 21² = |
| d) | 24² = |
Gib die Quadratzahlen an!
| a) | 16² = 256 |
| b) | 19² = 361 |
| c) | 21² = 441 |
| d) | 24² = 576 |
Körper
Wahr oder falsch? Begründe!
Wahr oder falsch? Begründe!
Wahr oder falsch? Begründe!
___________________________________________________________________________
___________________________________________________________________________
___________________________________________________________________________
Wahr oder falsch? Begründe!
Weitere Materialien
Umfang- Volumen- und Flächenberechnung
