Klausur Mathematik 10 90’ Thema: Trigonometrische Funktionen und deren Anwendung ___________________________________________________________________________
Name: .............................................. Klasse:............... Datum:............
Belehrende Hinweise:
Die Arbeit umfasst 8 thematische Aufgabenstellungen.
Bitte lösen Sie die Ihnen vorliegenden Aufgaben sauber und ordentlich; die Form
der Arbeit geht zu 10 % in die Zensur dieser Leistungsüberprüfung ein. Bitte halten Sie einen Korrekturrand von mindestens 3 cm ein. Alle Lösungen zu den Aufgabenstellungen sind zu nummerieren. Rechenwege müssen nachvollziehbar sein; ein der Aufgabe getreuer Antwortsatz ist
zu formulieren. Zwischen den Lösungen für die Aufgaben ist für Notationen zwei Zeilen frei zu
lassen. Jedes Blatt ist mit dem Namen zu versehen. Die Anzahl der beschriebenen Seiten ist hier anzugeben.
Die Arbeit umfasst.......... Seiten.
Die Aufgabenstellung ist unnummeriert als Anhang abzugeben. Schwerwiegende und gehäufte Verstöße gegen die sprachliche Richtigkeit und die
deutsche Rechtschreibung führen zum Abzug von Punkten. Bei Betrug oder Betrugsversuchen erfolgt unwiderruflich die Erteilung der Zensur
„6“ oder „00“ Punkte. Es werden ab dem Zeitpunkt der Vorlage der Arbeitsmaterialien keine Fragen mehr
beantwortet, da dies nicht als nötig erachtet wird und die individuell-
psychologische Fähigkeit der Selbständigkeit fördern soll. Viel Erfolg!
Auswertung in Bewertungseinheiten / Notenpunkten:
Nr. Bemerkung Soll Ist
1 6
2 3
3 2
4 1
5 6
6 13
7 5
8 9
Gesamt Gesamtpunkte im Inhalt 45 BE ______x 0,9 = _____ (I)
Form: _____ Notenpunkte x 0,1 = _____ (II)
Gesamtzensur: (I)+(II)= ______ ______
Name: .............................................. Klasse:............... Datum:............
Belehrende Hinweise:
Die Arbeit umfasst 8 thematische Aufgabenstellungen.
Bitte lösen Sie die Ihnen vorliegenden Aufgaben sauber und ordentlich; die Form
der Arbeit geht zu 10 % in die Zensur dieser Leistungsüberprüfung ein. Bitte halten Sie einen Korrekturrand von mindestens 3 cm ein. Alle Lösungen zu den Aufgabenstellungen sind zu nummerieren. Rechenwege müssen nachvollziehbar sein; ein der Aufgabe getreuer Antwortsatz ist
zu formulieren. Zwischen den Lösungen für die Aufgaben ist für Notationen zwei Zeilen frei zu
lassen. Jedes Blatt ist mit dem Namen zu versehen. Die Anzahl der beschriebenen Seiten ist hier anzugeben.
Die Arbeit umfasst.......... Seiten.
Die Aufgabenstellung ist unnummeriert als Anhang abzugeben. Schwerwiegende und gehäufte Verstöße gegen die sprachliche Richtigkeit und die
deutsche Rechtschreibung führen zum Abzug von Punkten. Bei Betrug oder Betrugsversuchen erfolgt unwiderruflich die Erteilung der Zensur
„6“ oder „00“ Punkte. Es werden ab dem Zeitpunkt der Vorlage der Arbeitsmaterialien keine Fragen mehr
beantwortet, da dies nicht als nötig erachtet wird und die individuell-
psychologische Fähigkeit der Selbständigkeit fördern soll. Viel Erfolg!
Auswertung in Bewertungseinheiten / Notenpunkten:
Nr. Bemerkung Soll Ist
1 6
2 3
3 2
4 1
5 6
6 13
7 5
8 9
Gesamt Gesamtpunkte im Inhalt 45 BE ______x 0,9 = _____ (I)
Form: _____ Notenpunkte x 0,1 = _____ (II)
Gesamtzensur: (I)+(II)= ______ ______
Klausur Mathematik 10 90’ Thema: Trigonometrische Funktionen und deren Anwendung ___________________________________________________________________________
Aufgabenstellungen 1/2
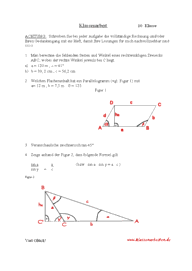
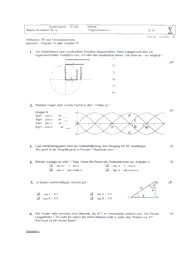
1.Rechne um! a) ins Bogenmaß: =34°, =405° b) in Winkel im Gradmaß: 1 = 1,5, 2= -0,45 2. Berechne und runde auf vier Nachkommastellen! a) sin ( 5/7 ) b) cos (-15° ) c) tan 2 3. Ermittle alle Winkel x mit O< x < 4 für die gilt: 4 sin (3x ) = - 4. 4. Gib die Gleichung der Funktion an! 5. Berechne die fehlenden Seiten und Winkel im Dreieck ( = 90° )!
Runde auf zwei Nachkommastellen!
= 53,1°; c = 5cm 6. Berechne die fehlenden Seiten und Winkel in einem Dreieck ABC! a) Konstruiere zunächst das Dreieck und fertige eine
Konstruktionsbeschreibung an! Führe die geforderten Berechnungen bei den gegebenen Größen
aus! a= 5,7cm, c=8cm, =56° b) a= 3,5cm, b=8cm, c= 6cm Berechne für dieses Dreieck zusätzlich den Flächeninhalt!
Aufgabenstellungen 1/2
1.Rechne um! a) ins Bogenmaß: =34°, =405° b) in Winkel im Gradmaß: 1 = 1,5, 2= -0,45 2. Berechne und runde auf vier Nachkommastellen! a) sin ( 5/7 ) b) cos (-15° ) c) tan 2 3. Ermittle alle Winkel x mit O< x < 4 für die gilt: 4 sin (3x ) = - 4. 4. Gib die Gleichung der Funktion an! 5. Berechne die fehlenden Seiten und Winkel im Dreieck ( = 90° )!
Runde auf zwei Nachkommastellen!
= 53,1°; c = 5cm 6. Berechne die fehlenden Seiten und Winkel in einem Dreieck ABC! a) Konstruiere zunächst das Dreieck und fertige eine
Konstruktionsbeschreibung an! Führe die geforderten Berechnungen bei den gegebenen Größen
aus! a= 5,7cm, c=8cm, =56° b) a= 3,5cm, b=8cm, c= 6cm Berechne für dieses Dreieck zusätzlich den Flächeninhalt!
Klausur Mathematik 10 90’ Thema: Trigonometrische Funktionen und deren Anwendung ___________________________________________________________________________
Aufgabenstellungen 2/2
7. Erkläre das Zustandekommen des Spezialfalles des Cosinussatzes
für = 90° und der damit verbundenen grundlegenden
mathematischen Regel für die Dreiecksberechnung! 8. Erläutere die Einwirkung der Parameter a, b und c der
Funktionsgleichung a sin (bx ) + c allgemein und anschließend anhand
von selbst gewählten Beispielen. Fertige dazu auch
Koordinatensysteme an!
___________________________________________________________________________ INHALT: 45-42-36-28-21-15-00 15 13 10 07 04 01 00 1+ 1- 2- 3- 4- 5- 6 FORM: 15 13 10 07 04 01 00 1+ 1- 2- 3- 4- 5- 6
Aufgabenstellungen 2/2
7. Erkläre das Zustandekommen des Spezialfalles des Cosinussatzes
für = 90° und der damit verbundenen grundlegenden
mathematischen Regel für die Dreiecksberechnung! 8. Erläutere die Einwirkung der Parameter a, b und c der
Funktionsgleichung a sin (bx ) + c allgemein und anschließend anhand
von selbst gewählten Beispielen. Fertige dazu auch
Koordinatensysteme an!
___________________________________________________________________________ INHALT: 45-42-36-28-21-15-00 15 13 10 07 04 01 00 1+ 1- 2- 3- 4- 5- 6 FORM: 15 13 10 07 04 01 00 1+ 1- 2- 3- 4- 5- 6
Lösungsvorschlag
Aufgabe 1a
Formel zur Umrechnung eines Winkels ins Bogenmaß :
Aufgabe 1b
Formel zur Umrechnung vom Bogenmaß in einen Winkel :
Aufgabe 2
In den Taschenrechner eingeben, richtige Einstellung auf Bogenmaß bzw. Winkelmaß
beachten: a) (Bogenmaß) b) (Winkelmaß) c) (Bogenmaß)
Aufgabe 3
Aufgabe 1a
Formel zur Umrechnung eines Winkels ins Bogenmaß :
Aufgabe 1b
Formel zur Umrechnung vom Bogenmaß in einen Winkel :
Aufgabe 2
In den Taschenrechner eingeben, richtige Einstellung auf Bogenmaß bzw. Winkelmaß
beachten: a) (Bogenmaß) b) (Winkelmaß) c) (Bogenmaß)
Aufgabe 3
Aufgabe 4
Begründung:
Verschiebt man die Funktion um 0,5 nach oben, geht sie exakt durch den Ursprung (0|0), ist
daher eine Sinus- und keine Cosinusfunktion
Die eben genannte Verschiebung der Sinusfunktion um 0,5 nach unten begründet die "-0,5"
am Ende der Funktion
Die Funktion ist auf die halbe Höhe zusammengestaucht (zwischen 0 und -1 anstatt zwischen
1 und -1). Daher der Faktor "0,5" vor dem Sinus
Aufgabe 5
Gegeben: Gesucht:
Begründung:
Verschiebt man die Funktion um 0,5 nach oben, geht sie exakt durch den Ursprung (0|0), ist
daher eine Sinus- und keine Cosinusfunktion
Die eben genannte Verschiebung der Sinusfunktion um 0,5 nach unten begründet die "-0,5"
am Ende der Funktion
Die Funktion ist auf die halbe Höhe zusammengestaucht (zwischen 0 und -1 anstatt zwischen
1 und -1). Daher der Faktor "0,5" vor dem Sinus
Aufgabe 5
Gegeben: Gesucht:
Aufgabe 6a
Konstruktion des Dreiecks:
1. Zeichnen von : 2. Einzeichnen des Winkels : 3. Mit dem Zirkel die Länge abtragen: 4. Strecke b einzeichnen:
Berechnung der fehlenden Seiten und Winkel:
Gegeben: Gesucht: Berechne über Cosinussatz: Berechnung von α über Sinussatz:
Konstruktion des Dreiecks:
1. Zeichnen von : 2. Einzeichnen des Winkels : 3. Mit dem Zirkel die Länge abtragen: 4. Strecke b einzeichnen:
Berechnung der fehlenden Seiten und Winkel:
Gegeben: Gesucht: Berechne über Cosinussatz: Berechnung von α über Sinussatz:
Aufgabe 6b
Gegeben: Gesucht: Berechne α über Cosinussatz: Berechne β über Sinussatz: Berechnung des Flächeninhalts : Für die Höhe gilt: und daher: Somit ist der Flächeninhalt:
Aufgabe 7
Der Cosinussatz für lautet: Da ist, folgt hieraus: Dies ist der Satz des Pythagoras:
Gegeben: Gesucht: Berechne α über Cosinussatz: Berechne β über Sinussatz: Berechnung des Flächeninhalts : Für die Höhe gilt: und daher: Somit ist der Flächeninhalt:
Aufgabe 7
Der Cosinussatz für lautet: Da ist, folgt hieraus: Dies ist der Satz des Pythagoras:
Aufgabe 8
Erläuterung der Parameter in
Parameter a:
Streckt oder staucht die Funktion in der Höhe : Die Funktion wird in der Höhe gestreckt : Die Funktion wird in der Höhe gestaucht : Die Funktion wird "auf den Kopf" gestellt
Beispiel:
Parameter b:
Verändert die Periodenlänge der Funktion : Die Periodenlänge wird kürzer : Die Periodenlänge wird größer : Die Funktion wird wieder "auf den Kopf" gestellt, da
Beispiel:
Erläuterung der Parameter in
Parameter a:
Streckt oder staucht die Funktion in der Höhe : Die Funktion wird in der Höhe gestreckt : Die Funktion wird in der Höhe gestaucht : Die Funktion wird "auf den Kopf" gestellt
Beispiel:
Parameter b:
Verändert die Periodenlänge der Funktion : Die Periodenlänge wird kürzer : Die Periodenlänge wird größer : Die Funktion wird wieder "auf den Kopf" gestellt, da
Beispiel: