www.Klassenarbeiten.de Seite 1
Klasse 10.GYM Klassenarbeit aus der Mathematik
Potenzen-Potenzfunktionen
Name:
Aufgabe 1 (voraussichtlich: 14 Punkte)
Vereinfache Sie soweit
wie möglich:
(a) ( ) 336
x (b) 12
5
4 3
43 2 16 aa
aa
a
−
(c) 4
3
3
4
22
15
8
27
16
25
9 −
z
x
z
y
y
x (d) ( )3144 )1()1( +−−− nn
Aufgabe 2 (voraussichtlich: 8 Punkte)
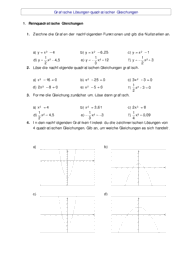
(a) Ordnen Sie den vier abgebildeten Graphen G1, G2, G3 und G4 jeweils einen der folgenden Funktions-
terme zu: (ca. 4 Punkte) 4
1 )( xxf =
4
2 )( −= xxf 5
1
3 )( xxf = 5
4 )( xxf = 5
5 )( −=xxf 5
6 3)( xxf =
5
1
7 )( xxf −= 8
8 )( −= xxf 5
1
9 2)( xxf −= 9
10 )( −= xxf
(b) Bestimmen Sie die Anzahl der Lösungen der folgenden Gleichung über : ( ) 111 2
3 −=+ xx.
Skizzieren Sie dazu die Graphen der Funktionen ( )31)( += xxf und 11)( 2 −= xxg in einem gemein-
samen Koordinatensystem (saubere und übersichtliche Skizze!). (ca. 4 Punkte)
Bitte wenden!
Klasse 10.GYM Klassenarbeit aus der Mathematik
Potenzen-Potenzfunktionen
Name:
Aufgabe 1 (voraussichtlich: 14 Punkte)
Vereinfache Sie soweit
wie möglich:
(a) ( ) 336
x (b) 12
5
4 3
43 2 16 aa
aa
a
−
(c) 4
3
3
4
22
15
8
27
16
25
9 −
z
x
z
y
y
x (d) ( )3144 )1()1( +−−− nn
Aufgabe 2 (voraussichtlich: 8 Punkte)
(a) Ordnen Sie den vier abgebildeten Graphen G1, G2, G3 und G4 jeweils einen der folgenden Funktions-
terme zu: (ca. 4 Punkte) 4
1 )( xxf =
4
2 )( −= xxf 5
1
3 )( xxf = 5
4 )( xxf = 5
5 )( −=xxf 5
6 3)( xxf =
5
1
7 )( xxf −= 8
8 )( −= xxf 5
1
9 2)( xxf −= 9
10 )( −= xxf
(b) Bestimmen Sie die Anzahl der Lösungen der folgenden Gleichung über : ( ) 111 2
3 −=+ xx.
Skizzieren Sie dazu die Graphen der Funktionen ( )31)( += xxf und 11)( 2 −= xxg in einem gemein-
samen Koordinatensystem (saubere und übersichtliche Skizze!). (ca. 4 Punkte)
Bitte wenden!
www.Klassenarbeiten.de Seite 2
Aufgabe 3 (voraussichtlich: 8 Punkte)
(a) Bei einer Kapitalanlage wächst ein Startvermögen von 1000€ in 20 Jahren auf 2653,30€ an.
Wie groß ist die Rendite der Kapitalanlage? (ca. 3 Punkte)
(b) Angenommen das Starguthaben von 1000€ würde nicht angelegt, sondern 20 Jahre lang in einem
Sparstrumpf versteckt. Berechnen Sie die Kaufkraft des Starguthabens in 20 Jahren, wenn man eine
Inflationsrate von 1% (2%, 3%, 4%, 6%, 8%, 10%,12%) unterstellt.
Tragen Sie Ihre Ergebnisse in eine Wertetabelle für die Funktion:
Inflationsrate --- Wert des Starguthabens nach 20 Jahren
ein und zeichnen Sie den zugehörigen Graphen in ein geeignetes Koordinatensystem.
Lesen Sie aus dem Graphen näherungsweise ab, bei welcher Inflationsrate das Startguthaben nur noch
die Hälfte seiner ursprünglichen Kaufkraft besitzt. (ca. 5 Punkte)
Aufgabe 3 (voraussichtlich: 8 Punkte)
(a) Bei einer Kapitalanlage wächst ein Startvermögen von 1000€ in 20 Jahren auf 2653,30€ an.
Wie groß ist die Rendite der Kapitalanlage? (ca. 3 Punkte)
(b) Angenommen das Starguthaben von 1000€ würde nicht angelegt, sondern 20 Jahre lang in einem
Sparstrumpf versteckt. Berechnen Sie die Kaufkraft des Starguthabens in 20 Jahren, wenn man eine
Inflationsrate von 1% (2%, 3%, 4%, 6%, 8%, 10%,12%) unterstellt.
Tragen Sie Ihre Ergebnisse in eine Wertetabelle für die Funktion:
Inflationsrate --- Wert des Starguthabens nach 20 Jahren
ein und zeichnen Sie den zugehörigen Graphen in ein geeignetes Koordinatensystem.
Lesen Sie aus dem Graphen näherungsweise ab, bei welcher Inflationsrate das Startguthaben nur noch
die Hälfte seiner ursprünglichen Kaufkraft besitzt. (ca. 5 Punkte)
www.Klassenarbeiten.de Seite 3
Lösungen
Aufgabe 1 (voraussichtlich: 14 Punkte)
(a) ( ) xx =
336 (b) aaa
aa
a −=
−
12
5
4 3
43 2 16
(c) 315
8
27
16
25
9 4
3
3
4
22 y
z
x
z
y
y
x =
− (d) ( ) 8)1()1( 3144 =−−− +nn
Aufgabe 2 (voraussichtlich: 8 Punkte)
(a) G2 ist eine Parabel zu einer Potenz mit einem positiven, ungeraden Exponenten. Da G2 durch den
Punkt (1|3) gehört G2 zum Funktionsterm5
6 3)( xxf = . G3 ist nur auf ℝ≥0 definiert und ist der Graph
einer Wurzelfunktion. Da G3 den Punkt (1|-1) enthält gehört G3 zum Funktionsterm5
1
7 )( xxf −= . G1
und G4 sind Hyperbeln zu Potenzen mit einem negativen, „ungeraden“ Exponenten. Da G4 im Bereich
x>1 schneller abfällt als G1, gehört G4 zum Funktionsterm 9
10 )( −= xxf und G1 zum Funktionsterm 5
5 )( −=xxf
.
(b) Es gibt 3 Schnittpunkte bzw. Lösungen der Gleichung.
Aufgabe 3 (voraussichtlich: 8 Punkte)
(a) Eine Einmalanlage eines Vermögens V liefert bei einer Rendite von r (in Prozent) nach n Jahren ein
Vermögen von ( )nr
n VV 1001 +=. Daraus berechnet sich die Rendite zu ( ) %00,5%10016533,21001 20 −=
−= n n
V
Vr
.
Lösungen
Aufgabe 1 (voraussichtlich: 14 Punkte)
(a) ( ) xx =
336 (b) aaa
aa
a −=
−
12
5
4 3
43 2 16
(c) 315
8
27
16
25
9 4
3
3
4
22 y
z
x
z
y
y
x =
− (d) ( ) 8)1()1( 3144 =−−− +nn
Aufgabe 2 (voraussichtlich: 8 Punkte)
(a) G2 ist eine Parabel zu einer Potenz mit einem positiven, ungeraden Exponenten. Da G2 durch den
Punkt (1|3) gehört G2 zum Funktionsterm5
6 3)( xxf = . G3 ist nur auf ℝ≥0 definiert und ist der Graph
einer Wurzelfunktion. Da G3 den Punkt (1|-1) enthält gehört G3 zum Funktionsterm5
1
7 )( xxf −= . G1
und G4 sind Hyperbeln zu Potenzen mit einem negativen, „ungeraden“ Exponenten. Da G4 im Bereich
x>1 schneller abfällt als G1, gehört G4 zum Funktionsterm 9
10 )( −= xxf und G1 zum Funktionsterm 5
5 )( −=xxf
.
(b) Es gibt 3 Schnittpunkte bzw. Lösungen der Gleichung.
Aufgabe 3 (voraussichtlich: 8 Punkte)
(a) Eine Einmalanlage eines Vermögens V liefert bei einer Rendite von r (in Prozent) nach n Jahren ein
Vermögen von ( )nr
n VV 1001 +=. Daraus berechnet sich die Rendite zu ( ) %00,5%10016533,21001 20 −=
−= n n
V
Vr
.
www.Klassenarbeiten.de Seite 4
(b)
Inflationsrate 1,0% 2,0% 3,0% 4,0% 6,0% 8,0% 10,0% 12,0%
Kaufkraft nach 20 Jahren 819,54 € 672,97 € 553,68 € 456,39 € 311,80 € 214,55 € 148,64 € 103,67 €
Ein Startvermögen V besitzt bei einer Inflationsrate von p (in Prozent) nach n Jahren noch eine
Kaufkraft von ( )np
n VV 1001/ +=. Daraus berechnet sich die Inflationsrate zu ( ) %53,3%100121001 20 −=
−= n
nV
Vp
.
(b)
Inflationsrate 1,0% 2,0% 3,0% 4,0% 6,0% 8,0% 10,0% 12,0%
Kaufkraft nach 20 Jahren 819,54 € 672,97 € 553,68 € 456,39 € 311,80 € 214,55 € 148,64 € 103,67 €
Ein Startvermögen V besitzt bei einer Inflationsrate von p (in Prozent) nach n Jahren noch eine
Kaufkraft von ( )np
n VV 1001/ +=. Daraus berechnet sich die Inflationsrate zu ( ) %53,3%100121001 20 −=
−= n
nV
Vp
.