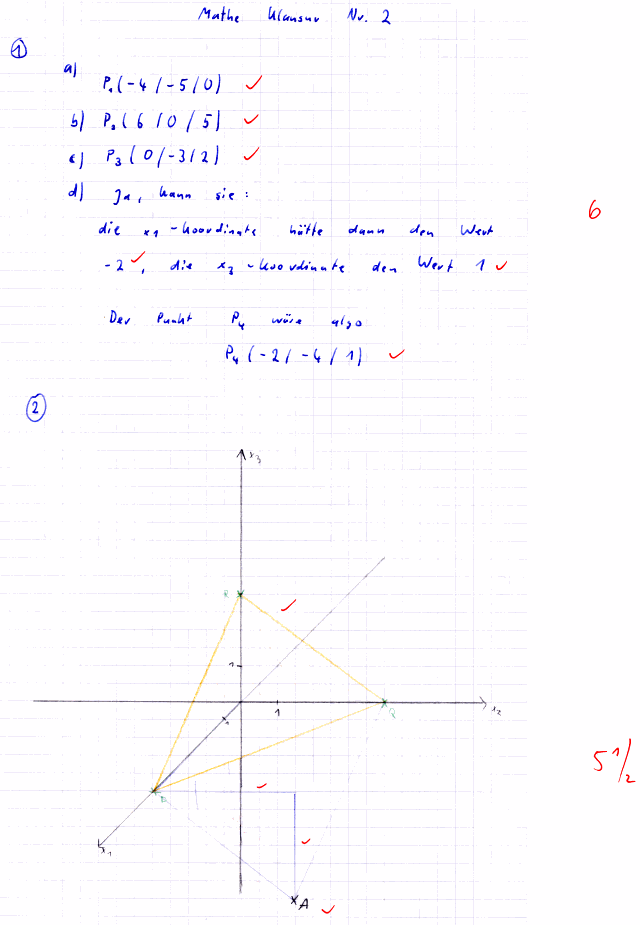
Ebene und Koordinate
Eine Ebene ist in der Mathematik ein flaches, zweidimensionales Objekt. Sie erstreckt sich unendlich weit in alle Richtungen. Du kannst dir eine Ebene als eine unendlich große, flache Oberfläche vorstellen. In einer Ebene können geometrische Objekte, wie Punkte, Linien und Vektoren abegebildet werden.
Um eine Ebene mathematisch zu beschreiben, benötigen wir mindestens drei Punkte, die nicht auf einer Geraden liegen. Mit diesen drei Punkten kann eine Ebene eindeutig definiert werden. Denn wenn die Ebene durch alle drei Punkte verläuft, entsteht nur eine einzige mögliche Ebene. Alternativ genügen ein Punkt und zwei Richtungsvektoren, die nicht parallel zueinander sind, um eine Ebene zu beschreiben.
Ebenen werden in der Regel mit einer Gleichung angegeben, die alle Punkte (x, y, z) in der Ebene erfüllen. Die allgemeine Form einer solchen Ebenengleichung ist:
Ax + By + Cz = D
Dabei sind A, B, C und D Konstanten und (x, y, z) sind die Koordinaten eines Punktes in der Ebene.
Eine Koordinate ist eine Zahl oder ein Satz von Zahlen, mit der die Position eines Punktes im Raum exakt beschrieben wird. Mit einer Koordinate kannst du einen Punkte innerhalb eines Koordinatensystems lokalisieren und genau identifizieren.
Koordinatensysteme sind Raster für geometrische Objekte, wie Punkte, Linien und Flächen. Das bekannteste Koordinatensystem ist das kartesische Koordinatensystem, das vom französischen Mathematiker René Descartes erfunden wurde. In diesem System haben wir Achsen, die als x-Achse, y-Achse und in einem dreidimensionalen Raum zusätzlich als z-Achse bezeichnet werden. Die Achsen schneiden sich im sogenannten Ursprung, der die Koordinaten (0, 0) im zweidimensionalen Raum oder (0, 0, 0) im dreidimensionalen Raum hat.
Um die Koordinaten eines Punktes in einem zweidimensionalen kartesischen Koordinatensystem zu bestimmen, benötigen wir zwei Zahlen: den x-Wert und den y-Wert. Der x-Wert gibt den Abstand des Punktes von der y-Achse an, während der y-Wert den Abstand des Punktes von der x-Achse angibt. In einem dreidimensionalen Raum kommt eine z-Achse hinzu, die senkrecht auf der xy-Ebene steht. Um die Koordinaten eines Punktes in diesem Raum zu bestimmen, benötigen wir drei Zahlen: x, y und z. Diese Zahlen geben die Position des Punktes in Bezug auf die drei Achsen exakt an.