M9b Klassenarbeit Nr.3, 07.04.2005 mit L ̈osung
Aufgabe 1)
Gegeben ist ein Dreieck ABC durch A(0/0), B(3/4) und C(8/8).
a)
Zeichne das Dreieck in ein Koordinatensystem und berechne den Umfang des Dreiecks.
b)
Untersuche ob das Dreieck rechtwinklig ist.
Aufgabe 2
Eine T ̈ur ist 82 cm breit und 1,97 m hoch.
Eine 2,10 m breite und 3,40 m lange Holzplatte soll durch die T ̈ur getragen werden. Ist das
m ̈oglich? Begr ̈unde durch Rechung. (Hilfe: Fertige eine Skizze an.)
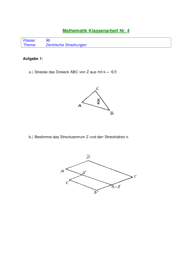
Aufgabe 3) Zeichne das Dreieck mit A(-1/0), B(3/-1), C(2/2) und das Streckzentrum S(1/1)
in ein Koordinatensystem (1 LE = 2 cm).
Dieses Dreieck hat einen Umfang von 11 cm. Das gestreckte Dreieck soll einen Umfang von 22
3
haben.
a)
Berechne den Streckfaktor k.
b)
Strecke das Dreieck mit diesem Streckfaktor.
c)
Bestimme den Fl ̈acheninhalt des urspr ̈unglichen und des gestrecken Dreiecks. Zeichne die
hierf ̈ur ben ̈
otigten Gr ̈
oßen ein und messe diese dann ab.
1
Aufgabe 1)
Gegeben ist ein Dreieck ABC durch A(0/0), B(3/4) und C(8/8).
a)
Zeichne das Dreieck in ein Koordinatensystem und berechne den Umfang des Dreiecks.
b)
Untersuche ob das Dreieck rechtwinklig ist.
Aufgabe 2
Eine T ̈ur ist 82 cm breit und 1,97 m hoch.
Eine 2,10 m breite und 3,40 m lange Holzplatte soll durch die T ̈ur getragen werden. Ist das
m ̈oglich? Begr ̈unde durch Rechung. (Hilfe: Fertige eine Skizze an.)
Aufgabe 3) Zeichne das Dreieck mit A(-1/0), B(3/-1), C(2/2) und das Streckzentrum S(1/1)
in ein Koordinatensystem (1 LE = 2 cm).
Dieses Dreieck hat einen Umfang von 11 cm. Das gestreckte Dreieck soll einen Umfang von 22
3
haben.
a)
Berechne den Streckfaktor k.
b)
Strecke das Dreieck mit diesem Streckfaktor.
c)
Bestimme den Fl ̈acheninhalt des urspr ̈unglichen und des gestrecken Dreiecks. Zeichne die
hierf ̈ur ben ̈
otigten Gr ̈
oßen ein und messe diese dann ab.
1
M9b Klassenarbeit Nr.3, 07.04.2005 mit L ̈osung
Aufgabe 1)
Gegeben ist ein Dreieck ABC durch A(0/0), B(3/4) und C(8/8).
a)
Zeichne das Dreieck in ein Koordinatensystem und berechne den Umfang des Dreiecks.
L ̈osung:
Abbildung 1: Aufgabe 1
Um den Umfang zu berechnen muss man jede einzelne Seite ̈uber Pythagoras berechnen:
a= BC= √52+ 42= √41 = 6,4 cm (1)
b= AC= √82+ 82= √128 = 11,3 cm (2)
c= AB= √32+ 42= √25 = 5 cm (3)
(4)
Der Umfang ist dann:
U= a+ b+ c= 22,7 cm (5)
1
Aufgabe 1)
Gegeben ist ein Dreieck ABC durch A(0/0), B(3/4) und C(8/8).
a)
Zeichne das Dreieck in ein Koordinatensystem und berechne den Umfang des Dreiecks.
L ̈osung:
Abbildung 1: Aufgabe 1
Um den Umfang zu berechnen muss man jede einzelne Seite ̈uber Pythagoras berechnen:
a= BC= √52+ 42= √41 = 6,4 cm (1)
b= AC= √82+ 82= √128 = 11,3 cm (2)
c= AB= √32+ 42= √25 = 5 cm (3)
(4)
Der Umfang ist dann:
U= a+ b+ c= 22,7 cm (5)
1
b)
Untersuche ob das Dreieck rechtwinklig ist.
L ̈osung:
Wir pr ̈ufen mit jede Ecke mit Pythagoras:
•Ecke A:
41 6= 128 + 25
⇒Kein Rechter Winkel!
•Ecke B:
128 6= 25 + 41
⇒Kein Rechter Winkel!
•Ecke C:
25 6= 128 + 41
⇒Kein Rechter Winkel!
Aufgabe 2
Eine T ̈ur ist 82 cm breit und 1,97 m hoch.
Eine 2,10 m breite und 3,40 m lange Holzplatte soll durch die T ̈ur getragen werden. Ist das
m ̈oglich? Begr ̈unde durch Rechung. (Hilfe: Fertige eine Skizze an.)
L ̈osung:
2
Untersuche ob das Dreieck rechtwinklig ist.
L ̈osung:
Wir pr ̈ufen mit jede Ecke mit Pythagoras:
•Ecke A:
41 6= 128 + 25
⇒Kein Rechter Winkel!
•Ecke B:
128 6= 25 + 41
⇒Kein Rechter Winkel!
•Ecke C:
25 6= 128 + 41
⇒Kein Rechter Winkel!
Aufgabe 2
Eine T ̈ur ist 82 cm breit und 1,97 m hoch.
Eine 2,10 m breite und 3,40 m lange Holzplatte soll durch die T ̈ur getragen werden. Ist das
m ̈oglich? Begr ̈unde durch Rechung. (Hilfe: Fertige eine Skizze an.)
L ̈osung:
2
Abbildung 2: T ̈ure
Man kann evtl die Holzplatte schr ̈ag stellen und durch die Diagonale der T ̈ure tragen. Um das
zu pr ̈ufen, muss man gucken, ob die Diagonale dder T ̈ure kleiner ist als die breite b= 2,10 m
der Holzplatte.
d= √(0,82 m)2+ (1,97 m)2(6)
= 2,13 m (7)
⇒2,10 m <2,13 m (8)
Das Holzbrett passt also durch die T ̈ure.
Aufgabe 3) Zeichne das Dreieck mit A(-1/0), B(3/-1), C(2/2) und das Streckzentrum S(1/1)
in ein Koordinatensystem.
Dieses Dreieck hat einen Umfang von 11 cm. Das gestreckte Dreieck soll einen Umfang von 22
3
haben.
L ̈osung:
3
Man kann evtl die Holzplatte schr ̈ag stellen und durch die Diagonale der T ̈ure tragen. Um das
zu pr ̈ufen, muss man gucken, ob die Diagonale dder T ̈ure kleiner ist als die breite b= 2,10 m
der Holzplatte.
d= √(0,82 m)2+ (1,97 m)2(6)
= 2,13 m (7)
⇒2,10 m <2,13 m (8)
Das Holzbrett passt also durch die T ̈ure.
Aufgabe 3) Zeichne das Dreieck mit A(-1/0), B(3/-1), C(2/2) und das Streckzentrum S(1/1)
in ein Koordinatensystem.
Dieses Dreieck hat einen Umfang von 11 cm. Das gestreckte Dreieck soll einen Umfang von 22
3
haben.
L ̈osung:
3
Abbildung 3: Ursprungsdreieck
a)
Berechne den Streckfaktor k.
L ̈osung:
Der Streckfaktor kergibt sich aus dem Verh ̈altnis der Umf ̈ange:
k= 22/3 cm
11 cm (9)
= 2
3 (10)
b)
Strecke das Dreieck mit diesem Streckfaktor.
L ̈osung:
4
a)
Berechne den Streckfaktor k.
L ̈osung:
Der Streckfaktor kergibt sich aus dem Verh ̈altnis der Umf ̈ange:
k= 22/3 cm
11 cm (9)
= 2
3 (10)
b)
Strecke das Dreieck mit diesem Streckfaktor.
L ̈osung:
4
Abbildung 4: Ursprungsdreieck in blau; Gestrecktes Dreieck in rot; Mit Konstruktions-Hilfen
c)
Bestimme den Fl ̈acheninhalt des urspr ̈unglichen und des gestrecken Dreiecks. Zeichne die
hierf ̈ur ben ̈otigten Gr ̈oßen ein und messe diese dann ab.
L ̈osung:
Der Fl ̈acheninhalt eines Dreiecks berechnet sich mit der Grundseite gund der darauf senkrecht
stehenden H ̈ohe hgnach:
A= g·hg
2 (11)
In unserem Fall sei die Grundseite mal c bzw. c’. Die H ̈ohen sind in der folgenden Abbildung
eingezeichnet.
5
c)
Bestimme den Fl ̈acheninhalt des urspr ̈unglichen und des gestrecken Dreiecks. Zeichne die
hierf ̈ur ben ̈otigten Gr ̈oßen ein und messe diese dann ab.
L ̈osung:
Der Fl ̈acheninhalt eines Dreiecks berechnet sich mit der Grundseite gund der darauf senkrecht
stehenden H ̈ohe hgnach:
A= g·hg
2 (11)
In unserem Fall sei die Grundseite mal c bzw. c’. Die H ̈ohen sind in der folgenden Abbildung
eingezeichnet.
5
Abbildung 5: Ursprungsdreieck in blau; Gestrecktes Dreieck in rot; H ̈ohen gestrichelt
Die H ̈ohe von des Ursprungsdreiecks ist h= 5,4 cm.
Die H ̈ohe des gestreckten Dreiecks ist h′= 3,6 cm, was sich nicht nur durch Ausmessen, son-
dern auch durch Multiplizieren mit dem Streckfaktor 2/3 ergibt.
Die Grundseite cdes Ursprungsdreiecks betr ̈agt c= 8,2 cm. Messen oder Multiplizieren mit
2/3 gibt die Grundseite des gestreckten Dreiecks: c′= 5,5 cm.
Der Fl ̈acheninhalt des Ursprungsdreiecks ist A= 22,14 cm2.
Der Fl ̈acheninhalt des gestreckten Dreiecks ist A= 9,9 cm2.
L ̈osung bei MH (c) 2005
6
Die H ̈ohe von des Ursprungsdreiecks ist h= 5,4 cm.
Die H ̈ohe des gestreckten Dreiecks ist h′= 3,6 cm, was sich nicht nur durch Ausmessen, son-
dern auch durch Multiplizieren mit dem Streckfaktor 2/3 ergibt.
Die Grundseite cdes Ursprungsdreiecks betr ̈agt c= 8,2 cm. Messen oder Multiplizieren mit
2/3 gibt die Grundseite des gestreckten Dreiecks: c′= 5,5 cm.
Der Fl ̈acheninhalt des Ursprungsdreiecks ist A= 22,14 cm2.
Der Fl ̈acheninhalt des gestreckten Dreiecks ist A= 9,9 cm2.
L ̈osung bei MH (c) 2005
6